Practical Max/min (1 Viewer)

[cutemouse]

The cost of running a car at an average speed of v km/h is given by 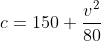cents per hour. Find the average speed, to the nearest km/h at which the cost of a 500km trip is a minimum.

Answer: 110km/h.

This may well be a 2U question. Hard to tell though since it's in a 2U/3U book.

 

[jet]

Can you please posts the source of your question?

Thanks.

 

[cutemouse]

Can you please posts the source of your question?

Math in Focus Challenge Ex 2.

Trying to write solutions for them lol.

 

[jet]

Here's how I see it:

This is a parabola. Parabolas have only one minimum; and this one has the minimum at the origin. This is the only value which makes sense, because 150 cents is the smallest value the cost can carry.

Factoring in the idea that v = 500/t, we get an hyperbola which has a minimum value at t --> infinity, which exactly corresponds to the value v = 0. I think you need an extra piece of restraining information.

 

[cutemouse]

Apparently not... I think you have to use the fact the trip is 500 km somehow and maybe something else :S

 

[xV1P3R]

t = 500/v
c = 150 + v²/80

Let C be total cost
C = c.t (cost/time x time)
C = (150 + v²/80)(500/v)
C = 75000v^(-1) + 25v/4
dC/dv = -75000v^(-2) + 25/4

For poss SP to occur, dC/dv = 0
-75000v^(-2) + 25/4 = 0
25v²/4 = 75000
v² = 12000
v = 109.5445 (v>0)
Therefore SP occurs at v

d²C/dv² = 150000v^(-3)
Test nature
v = 109.5445
d²C/dv² = 0.1141089 > 0
Therefore concave upwards and since a SP, therefore rel min TP occurs at v = 109.5445
As there are no other SP's in the domain v>0 and since function is continuous
Therefore absolute min value of C occurs at v = 109.5445

 

[jet]

d²C/dv² = 150000v^(-3)
Test nature
v = 109.5445
d²C/dv² = 0.1141089 > 0
Therefore concave upwards and since a SP, therefore rel min TP occurs at v = 109.5445
As there are no other SP's in the domain v>0 and since function is continuous
Therefore absolute min value of C occurs at v = 109.5445

Nice work, but a word of caution; testing the nature of a stationary point using the second derivative is NOT enough to conclude whether it is a maximum or a minimum.

For example, take the curve y = x⁴. The second derivative test tells you it has a horizontal point of inflexion, which in truth, it doesn't.

The only way of confirming the nature of a stationary point is by considering the sign-change of the first derivative across the stationary point.

 

[study-freak]

Nice work, but a word of caution; testing the nature of a stationary point using the second derivative is NOT enough to conclude whether it is a maximum or a minimum.

For example, take the curve y = x⁴. The second derivative test tells you it has a horizontal point of inflexion, which in truth, it doesn't.

The only way of confirming the nature of a stationary point is by considering the sign-change of the first derivative across the stationary point.

Actually, I think 2nd derivative test can conclusively test for the nature of max/min points, but for points of inflexion, we need to test for a change in concavity (as in sign change).

 

[Cazic]

The second derivative test can be a conclusive wrt to mins or maxs, but often isn't. The classic example y = x⁴ that jetblack gave doesn't play nice with that test.

 

[Lukybear]

The second derivative test can be a conclusive wrt to mins or maxs, but often isn't. The classic example y = x⁴ that jetblack gave doesn't play nice with that test.

I really doubt such Qs would be asked in 2/3 unit paper. And + using the second derivative to determine concavity is part of syllabus i think.

 

[study-freak]

The second derivative test can be a conclusive wrt to mins or maxs, but often isn't. The classic example y = x⁴ that jetblack gave doesn't play nice with that test.

oh lol
of course
I don't know what I was thinking some mins ago lol

 

[xV1P3R]

But is it safe to just go to second derivative test, if you get a non-zero leave it at that, if you get a zero, you go to first derivative test.

 

[cutemouse]

testing the nature of a stationary point using the second derivative is NOT enough to conclude whether it is a maximum or a minimum.

I think it is... that's how I was always taught (and is taught in many reputable textbooks such as Coroneos).

But if upon substitution of the abssica of the stat. pt, y''=0; this means no new information and you need to use the 1st deriv sign test to clarify its nature.

 

[jet]

In the syllabus BOS says they don't find it conclusive enough to use the second derivative test. They say it should be "used with caution". I was quite surprised to read this when I was teaching geometry of the derivative on Wednesday.

I was taught to always look for a change in sign on the first derivative. For some of the functions given to us it is extremely difficult to calculate the second derivative anyway. It's just easier in my opinion, and it's the way I will teach it to all my students.

But we all have our preference. This is just mine

 

[cutemouse]

In the syllabus BOS says they don't find it conclusive enough to use the second derivative test. They say it should be "used with caution". I was quite surprised to read this when I was teaching geometry of the derivative on Wednesday.

It should be used with caution because you can have a situation where y''=0 upon substitution.

I mean for most cubics (and quartics for that matter), in my opinion, you'd be crazy to test the nature using the first deriv test. This is especially since most curve sketching questions ask you to find the points of inflexion; which would require you to find the second derivative anyway.

 

[Trebla]

Alternatively, (if the first derivative is nice enough) just sketch the first derivative and you should be able to deduce the nature of turning points by looking at the neighbourhood of its x-intercepts.