The cost of running a car at an average speed of v km/h is given by 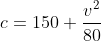 cents per hour. Find the average speed, to the nearest km/h at which the cost of a 500km trip is a minimum.
cents per hour. Find the average speed, to the nearest km/h at which the cost of a 500km trip is a minimum.
Answer: 110km/h.
This may well be a 2U question. Hard to tell though since it's in a 2U/3U book.
Answer: 110km/h.
This may well be a 2U question. Hard to tell though since it's in a 2U/3U book.

