HSC 2016 MX2 Integration Marathon (archive) (4 Viewers)

seanieg89 · Jan 15, 2016

Re: MX2 2016 Integration Marathon

Okay, would people like me to post a solution to my old one then? Or is anyone still trying it?

Drsoccerball · Jan 15, 2016

Re: MX2 2016 Integration Marathon

Can easily be solved by a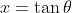 $x=\tan \theta$ substitution.
As a wise man named DJ Khaled once said

Another one:

$\int{\frac{1}{\sin{(x-\frac{\pi}{3}) \cdot \cos{x}}}} dx$

Drsoccerball · Jan 15, 2016

Re: MX2 2016 Integration Marathon

seanieg89 said:
Okay, would people like me to post a solution to my old one then? Or is anyone still trying it?

The one I said was 0

? Let me have a proper attempt.

seanieg89 · Jan 15, 2016

Re: MX2 2016 Integration Marathon

Drsoccerball said:
The one I said was 0 ? Let me have a proper attempt.

By all means, I think it's fairly fun

.

Will post my solution later if it remains unsolved here.

seanieg89 · Jan 16, 2016

Re: MX2 2016 Integration Marathon

Okay, I think it's been long enough so I will post my solution.

If you feel you are making progress then keep trying yourself before reading the below!!

For starters, let's assume a and b are positive, as changing the sign of one of these guys literally just changes the sign of the integral, as sine is odd.

$I=\lim_{R\rightarrow \infty}\int_{-R}^R \frac{\sin(ax)\sin(bx)}{x^2}\, dx\\ \\ = \lim_{R\rightarrow \infty}\int_{-R}^R \frac{\cos(a-b)x -\cos(a+b)x}{2x^2}\, dx \\ \\ = \lim_{R\rightarrow \infty}\int_{-R}^R \frac{\sin^2((a+b)x/2)-\sin^2((a-b)x/2)}{x^2}\, dx$

by basic trigonometric manipulations (specifically, product to differences and the half angle formula.) The motivation for the second manipulation is that the denominator tends to zero as x -> 0. This means that if we want to split the integral up as a sum or difference, the parts of the numerator should each tend to zero as well. so sines are good but cos's are bad.

So we have now reduced it to studying integrals of the form

$J(c)=\lim_{R\rightarrow \infty}\int_{-R}^R \frac{\sin^2(cx)}{x^2}\, dx\\ \\ =c\lim_{R\rightarrow \infty}\int_{-cR}^{cR} \frac{\sin^2(x)}{x^2}\, dx \\ \\ =c\lim_{R\rightarrow \infty}\int_{-cR}^{cR}\sin^2(x)\frac{d}{dx}(-1/x)\, dx\\ \\ =c\lim_{R\rightarrow \infty} \int_{-cR}^{cR} \frac{\sin(2x)}{x}\, dx\\ \\ = c\lim_{R\rightarrow \infty}\int_{-2cR}^{2cR}\frac{\sin(x)}{x}\, dx$

where the third inequality came from integrating by parts, noting that the boundary term decays as 1/R and hence vanishes in the limit.

Now it is tempting to conclude that this final quantity is nothing more than the principal value integral of sin(x)/x over the real line. HOWEVER, there is a subtlety caused by c's sign! Note that if c is negative, then this final integral is negatively oriented! This means that in this case we will actually get the negative of the principal value integral. Hence we have

$J(c)=\textrm{sgn(c)}\cdot c\pi$

where the sgn function is defined to be 1 on the positive reals, -1 on the negative reals, and 0 at zero.

Plugging this back into our most recent expression for I, we get

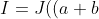$I=J((a+b)/2)-J((a-b)/2)=\frac{(a+b)\pi}{2}-\frac{(a-b)\pi}{2}\textrm{sgn}(a-b)\\ \\=\frac{(a+b)\pi}{2}-\frac{(\max(a,b)-\min(a,b))\pi}{2}\\ \\=\pi\cdot\min(a,b).$

The surprising upshot: the integral does not vary if you change the larger of the two parameters, but it does if you change the smaller one!

seanieg89 · Jan 16, 2016

Re: MX2 2016 Integration Marathon

Note that following my own suggestion, I assumed knowledge of the sin(x)/x integral in order to compute the above.

So treating it as a separate question, prove that:

$\lim_{R\rightarrow\infty}\int_{-R}^R\frac{\sin(x)}{x}\, dx=\pi$

I will give students a little more time to have a crack at this famous integral before I post an evaluation of it too.

seanieg89 · Jan 16, 2016

Re: MX2 2016 Integration Marathon

It is perhaps a bit much to expect a current student to tackle the above integral without hints, so here is a a rough walkthrough:

$1. Let $I_n=\int_{-\pi/2}^{\pi/2} \frac{\sin(2n+1)x}{x}\, dx$ and show that $I_n$ converges to the integral $I$ you are seeking.$

$2. Let $J_n=\int_{-\pi/2}^{\pi/2} \frac{\sin(2n+1)x}{\sin(x)}\, dx$ and write \\$J_n-I_n=\int_{-\pi/2}^{\pi/2} g(x)\sin(2n+1)x \, dx$ for some function $g$.$

$3. Prove that $g$ is differentiable, with continuous and bounded derivative in the interval. (This fact is not obvious. 1/sin(x) and 1/x both blow up at the origin, but the point is that taking their difference removes this singularity.) Use inequalities for the trig functions that come from repeated integration to prove this part.$

$4. Integrate by parts to get a good handle on $J_n-I_n$.$

$5. Tackle the easier integral $J_n$ that you have now reduced your problem to! What does $J_n$ tend to as $n\rightarrow\infty$? Use this to finally conclude your evaluation of the original integral $I$.$

omegadot · Jan 16, 2016

Re: MX2 2016 Integration Marathon

Drsoccerball said:
Can easily be solved by a $x=\tan \theta$ substitution.

$\noindent Particular care needs to be taken with the limits of integration. Would you care to post a solution for the benefit of others?$

omegadot · Jan 16, 2016

Re: MX2 2016 Integration Marathon

Drsoccerball said:
As a wise man named DJ Khaled once said

Another one:

$\int{\frac{1}{\sin{(x-\frac{\pi}{3}) \cdot \cos{x}}}} dx$

$\begin{align*} \int \frac{dx}{\sin (x - \frac{\pi}{3} ) \cdot \cos x} &= \int \frac{2 \sec x}{\sin x - \sqrt{3} \cos x} \, dx = 2 \int \frac{\sec^2 x}{\tan x - \sqrt{3}} \, dx\end{align*}$

$$\noindent Now let $u = \tan x, du = \sec^2 \, dx$. So$\\\begin{align*} \int \frac{dx}{\sin (x - \frac{\pi}{3} ) \cdot \cos x} &= 2 \int \frac{du}{u - \sqrt{3}}\\&= 2 \ln |u - \sqrt{3}| + \cal{C}\\&= 2 \ln|\tan x - \sqrt{3}| + \cal{C}\end{align*}$

$\noindent \textbf{Next Question}$

$$\noindent Find $\int \frac{\sin^2 x}{\sin x + 2\cos x} \, dx.$

Paradoxica · Jan 16, 2016

Re: MX2 2016 Integration Marathon

omegadot said:
$\noindent I think we need a \textbf{New Question}$

$$\noindent Evaluate $\int^{\sqrt{3}}_0 \sin^{-1} \left (\frac{2x}{1 + x^2} \right ) \, $d$x$

$$\noindent Observe that $\sin^{-1}\left(\frac{2x}{1+x^2}\right) \equiv 2\tan^{-1}x \; \forall \log |x| \in \mathbb{R}^- \\ $Observe that $\sin^{-1}\left(\frac{2x}{1+x^2}\right) \equiv 2\cot^{-1}x \; \forall \log |x| \in \mathbb{R}^+ \\ $This means we must split the integral into two segments at the non-differentiable $x$-value of $1$. The integral is now $ 2 \int_0^1 \tan^{-1} x $d$x +2 \int_1^{\sqrt{3}} \cot^{-1} x $d$x \\ $Integrating by parts on both expressions, we have $\int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \left [2x\tan^{-1}x \right ]_0^1 -\int_{0}^{1}\frac{2x}{1+x^2}$d$x+\left[2x\cot^{-1}x \right]_1^{\sqrt{3}}+\int_{1}^{\sqrt{3}}\frac{2x}{1+x^2}$d$x \\ \int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \left [2x\tan^{-1}x -\log(1+x^2) \right ]_0^1 +\left[2x\cot^{-1}x +\log(1+x^2) \right]_1^{\sqrt{3}}$

$\noindent$ \int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \frac{\pi}{2} - \log 2 + \frac{\pi}{\sqrt{3}} -\frac{\pi}{2} +2\log 2 - \log 2 = \frac{\pi}{\sqrt{3}} \\$Which matches the result returned by Wolfram Mathematica.$ \\ $Doctorsoccerball's naive substitution of $x = \tan \theta $ implicitly presumes that the integrand is identically equivalent to $2\tan^{-1} x$ for every real value of $x$. This is, of course false, as the absolute value of $\sin^{-1} x$ can never exceed $\frac{\pi}{2}$. This results in a number that is bigger than the true result.$

omegadot · Jan 16, 2016

Re: MX2 2016 Integration Marathon

Paradoxica said:
$$\noindent Observe that $\sin^{-1}\left(\frac{2x}{1+x^2}\right) \equiv 2\tan^{-1}x \; \forall \log |x| \in \mathbb{R}^- \\ $Observe that $\sin^{-1}\left(\frac{2x}{1+x^2}\right) \equiv 2\cot^{-1}x \; \forall \log |x| \in \mathbb{R}^+ \\ $This means we must split the integral into two segments at the non-differentiable $x$-value of $1$. The integral is now $ 2 \int_0^1 \tan^{-1} x $d$x +2 \int_1^{\sqrt{3}} \cot^{-1} x $d$x \\ $Integrating by parts on both expressions, we have $\int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \left [2x\tan^{-1}x \right ]_0^1 -\int_{0}^{1}\frac{2x}{1+x^2}$d$x+\left[2x\cot^{-1}x \right]_1^{\sqrt{3}}+\int_{1}^{\sqrt{3}}\frac{2x}{1+x^2}$d$x \\ \int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \left [2x\tan^{-1}x -\log(1+x^2) \right ]_0^1 +\left[2x\cot^{-1}x +\log(1+x^2) \right]_1^{\sqrt{3}}$

$\noindent$ \int_{0}^{\sqrt{3}} \sin^{-1}\left( \frac{2x}{1+x^2}\right )$d$x = \frac{\pi}{2} - \log 2 + \frac{\pi}{\sqrt{3}} -\frac{\pi}{2} +2\log 2 - \log 2 = \frac{\pi}{\sqrt{3}} \\$Which matches the result returned by Wolfram Mathematica.$ \\ $Doctorsoccerball's naive substitution of $x = \tan \theta $ presumes that the integrand is identically equivalent to $2\tan^{-1} x$ for every real value of $x$. This is, of course false, as the absolute value of $\sin^{-1} x$ can never exceed $\frac{\pi}{2}$. This results in a number that is bigger than the true result.$

$\noindent And is exactly why I selected the limits of integration I did!$

InteGrand · Jan 16, 2016

Re: MX2 2016 Integration Marathon

$\noindent We can use a Drsoccerball-like substitution of $x =\tan \frac{\theta}{2}, \theta \in (-\pi, \pi)$ $\Big{(}$so the new limits of integration become from $0$ to $\frac{2\pi}{3} \Big{)}$, it's just that we need to make sure we use the fact that $\sin^{-1} \left(\sin \theta \right) =\pi -\theta$ for part of the resultant integral, namely the part where $\frac{\pi}{2} \leq \theta \leq \frac{2\pi}{3}$.$

Paradoxica · Jan 16, 2016

Re: MX2 2016 Integration Marathon

omegadot said:
$\begin{align*} \int \frac{dx}{\sin (x - \frac{\pi}{3} ) \cdot \cos x} &= \int \frac{2 \sec x}{\sin x - \sqrt{3} \cos x} \, dx = 2 \int \frac{\sec^2 x}{\tan x - \sqrt{3}} \, dx\end{align*}$

$$\noindent Now let $u = \tan x, du = \sec^2 \, dx$. So$\\\begin{align*} \int \frac{dx}{\sin (x - \frac{\pi}{3} ) \cdot \cos x} &= 2 \int \frac{du}{u - \sqrt{3}}\\&= 2 \ln |u - \sqrt{3}| + \cal{C}\\&= 2 \ln|\tan x - \sqrt{3}| + \cal{C}\end{align*}$

$\noindent \textbf{Next Question}$

$$\noindent Find $\int \frac{\sin^2 x}{\sin x + 2\cos x} \, dx.$

Two words: Irreducibly Messy.

omegadot · Jan 17, 2016

Re: MX2 2016 Integration Marathon

Paradoxica said:
Two words: Irreducibly Messy.

$\noindent A final answer of $-\frac{4}{5 \sqrt{5}} \ln \left |\frac{\sqrt{5} + \cos x - 2 \sin x}{\sin x + 2 \cos x} \right | - \frac{1}{5} \cos x - \frac{2}{5} \sin x + \cal{C}$ looks pretty ``clean'' to me ;-)$

Paradoxica · Jan 17, 2016

Re: MX2 2016 Integration Marathon

omegadot said:
$\noindent \textbf{Next Question}$

$$\noindent Find $\int \frac{\sin^2 x}{\sin x + 2\cos x} \, dx.$

$$\noindent $I = \frac{1}{5}\int \frac{4\sin^2{x} + 4\cos^2{x} + \sin^2{x} - 4\cos^2{x}}{\sin{x} + 2\cos{x}} $d$x \\ I= \frac{1}{5}\int \frac{4}{\sin{x} + 2\cos{x}} + \sin{x}-2\cos{x} $d$x \\I = \frac{4}{5\sqrt{5}} \int \frac{\text{d}x}{\sin(x+\tan^{-1}2)} - \frac{\cos{x} + 2\sin{x}}{5} \\ -I = \frac{4}{5\sqrt{5}} \log (\csc(x+\tan^{-1}2) + \cot(x+\tan^{-1}2))+ \frac{\cos{x} + 2\sin{x}}{5} \\ -I = \frac{4}{5\sqrt{5}}\log\left(\frac{1+\cos(x+\tan^{-1}2)}{\sin(x+\tan^{-1}2)} \right)+ \frac{\cos{x} + 2\sin{x}}{5} \\-I = \frac{4}{5\sqrt{5}}\log\left(\frac{\sqrt{5}+\cos{x}+2\sin{x}}{\sin{x}+2\cos{x}}\right )+\frac{\cos{x} + 2\sin{x}}{5}$

Paradoxica · Jan 17, 2016

Re: MX2 2016 Integration Marathon

An extension of the previous problem, I guess...

$\noindent a) Show that it is always possible to decompose any expression of the form$\\ \frac{p\sin^2x +q\cos^2x +r\sin x\cos x}{a\sin x+b\cos x} \forall \{a,b,p,q,r \} \in \mathbb{R} $ (A.K.A. use partial fractions)$ \\$ into a sum of 3 simpler expressions, subject to restrictions on the denominator.$ \\ $b) Suppose $a^2 +b^2 = c^2$. Evaluate the integral of the above expression.$

Drsoccerball · Jan 17, 2016

Re: MX2 2016 Integration Marathon

Do we actually have to watch out for the domain in integration ?

InteGrand · Jan 17, 2016

Re: MX2 2016 Integration Marathon

Drsoccerball said:
Do we actually have to watch out for the domain in integration ?

Yeah.

leehuan · Jan 17, 2016

Re: MX2 2016 Integration Marathon

I haven't tried it yet.

$\\ $Find a reduction formula for $\int { \cos { { x }^{ \frac { 1 }{ n } } } dx } , n \in \mathbb N$

Paradoxica · Jan 17, 2016

Re: MX2 2016 Integration Marathon

leehuan said:
I haven't tried it yet.

$\\ $Find a reduction formula for $\int { \cos { { x }^{ \frac { 1 }{ n } } } dx } , n \in \mathbb N$

Requires multi-valued gamma function with one real and one imaginary argument, according to Mathematica. So a reduction formula definitely exists.

HSC 2016 MX2 Integration Marathon (archive) (4 Viewers)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Active Member

Active Member

-insert title here-

Active Member

Well-Known Member

-insert title here-

Active Member

-insert title here-

-insert title here-

Well-Known Member

Well-Known Member

Well-Known Member

-insert title here-

Users Who Are Viewing This Thread (Users: 0, Guests: 4)