SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
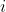 \frac{d}{dx}(e^x)=0+1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...) By differentiation.
By differentiation.
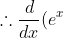=e^x)
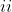\frac{d}{dx}\sin x = \cos x)
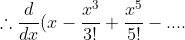=1-\frac{x^2}{2!}+\frac{x^4}{4!}...=\cos x)
b)
Let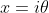
Solve from there. By using RHS then it will be in the form of LHS.
Laptop stuffing up so I can't type much.
For the last parts.
Use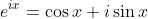
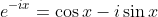
Substitute and solve.
b)
Let
Solve from there. By using RHS then it will be in the form of LHS.
Laptop stuffing up so I can't type much.
For the last parts.
Use
Substitute and solve.
Last edited:


