-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX2 Marathon (archive) (1 Viewer)
- Thread starter nightweaver066
- Start date
Re: 2012 HSC MX2 Marathon

Last edited:
lolcakes52
Member
- Joined
- Oct 31, 2011
- Messages
- 283
- Gender
- Undisclosed
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Second part is done with Newton's method for x=k to find the approximation. I'm having trouble with the first part, possibly because I'm not sure about whether the next root is between k=1 and 1, greater than k, or less than zero.
Second part is done with Newton's method for x=k to find the approximation. I'm having trouble with the first part, possibly because I'm not sure about whether the next root is between k=1 and 1, greater than k, or less than zero.
barbernator
Active Member
- Joined
- Sep 13, 2010
- Messages
- 1,435
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Well the sum of the roots is k, so if one root is between 0 and 1, one is between k-1 and k, then the next must be between 0 and 1 as well to satisfy kSecond part is done with Newton's method for x=k to find the approximation. I'm having trouble with the first part, possibly because I'm not sure about whether the next root is between k=1 and 1, greater than k, or less than zero.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
.Here is a decent question:
The three roots of the complex polynomial:
all lie on the unit circle in the complex plane. Prove that the three roots of:
also lie on the unit circle.
RealiseNothing
what is that?It is Cowpea
Re: 2012 HSC MX2 Marathon
:=z^3 + 3z^2 + 3z + 3)
y/n?
So far I've got:Here is a decent question:
The three roots of the complex polynomial:
all lie on the unit circle in the complex plane. Prove that the three roots of:
also lie on the unit circle.
y/n?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: 2012 HSC MX2 Marathon
I don't think q can possibly be that, that would imply that the product of roots of p has modulus 3.So far I've got:
y/n?
RealiseNothing
what is that?It is Cowpea
Re: 2012 HSC MX2 Marathon
Let the roots of p(x) be alpha, beta, and gamma. Then:
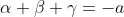
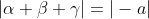
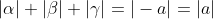

Since the roots lie on the unit circle and hence .
.
I then do this for 'b' and 'c' as well to obtain my expression for q(x).
Then what have I done wrong? Have I assumed something that isn't true maybe?I don't think q can possibly be that, that would imply that the product of roots of p has modulus 3.
Let the roots of p(x) be alpha, beta, and gamma. Then:
Since the roots lie on the unit circle and hence
I then do this for 'b' and 'c' as well to obtain my expression for q(x).
RealiseNothing
what is that?It is Cowpea
Re: 2012 HSC MX2 Marathon
triangular inequality fail.
oh shit.From your second line to your third line of displayed equations.
triangular inequality fail.
