I'll give you the first half of it, and let you finish it off.
For b):
It seems we need to somehow connect, a/b to b/a, b/c to c/b and c/a to a/c, so that we can get some 'cancellation' and get a definitive number.
One may then proceed to add something to both sides but this doesn't look like it will lead anywhere.
Now notice that if you multiply any 2 of the term,
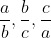
we will get one of these:
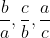
i.e. if you multiply the first 2 terms in the inequality that we need
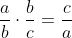
This is important since it will allow us to establish the connection, so how do we go from a sum:
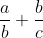
to a product? We can use the basic inequality:
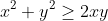
, we need an addition of 3 terms however, so lets add 3 of htose inequalities side by side to yield the familiar inequality:
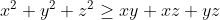
Substituting appropriate values in:
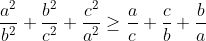
We don't really want to deal with the squares of a/b b/c and c/a, so lets force to to become just a/b b/c and c/a
^2 \geq 3\left(\frac{a}{c} + \frac{c}{b} + \frac{b}{a} \right ) )
I'll let you continue on from here however, if you've tried and can't get it I'll finish it off for you
======
c) Unfortunately, if we do something similar here to above, we will have to resort to using the inequality:
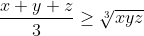
Which I don't want to do, nor do I think the HSC will accept it unless you prove it, if I were allowed to use this inequality then the first one becomes trivial, by just subbing in x=a/b, y=b/c, z=c/d
I'll post again if I can find another solution to this one.
EDIT: Please ignore completely, its pretty wrong =)