Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Why divide by 2! ? Theres no more repeats.In that case, I now have
)
EDIT: lel the word rat repeats...
Why divide by 2! ? Theres no more repeats.In that case, I now have
)
Answers on moodle
Would anyone know how to start off this one?
Firstly I did (n+k)|n^2 but I'm not sure how to proceed from there.
Sorry I know I can do this myself but I don't have time to right now. Can someone prove this?
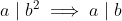
Okay so (n + k)|n^2
Would anyone know how to start off this one?
Firstly I did (n+k)|n^2 but I'm not sure how to proceed from there.
Oops. Well this was the question and the let us assume a result (potentially true upon the basis of primality though)

Man... need Peter Brown though... cause that's so not obvious to induce the diff. of two squares and the add/deduct trickOkay so (n + k)|n^2
n^2 = (n + k)M for some M integer.
Take note: n^2 = (n - k)(n + k) + k^2
(n + k)M = (n - k)(n + k) + k^2
(n + k)(M + k - n) = k^2
Therefore (n + k)|k^2
If k <= sqrt(n) that means n + k > k^2 and thus a contradiction (Take note k, n are positive integers)
Therefore k > sqrt(n)
Yeah I would've never got this in the exam...Man... need Peter Brown though... cause that's so not obvious to induce the diff. of two squares and the add/deduct trick
I thought everyone knew.Answers on moodle
Edit: omg i know who you are
You didn't try long division?Man... need Peter Brown though... cause that's so not obvious to induce the diff. of two squares and the add/deduct trick
I thought you were the one that hated long divisionYou didn't try long division?
gosh you people.
Yeah if p is a prime, then that's a true result.Oops. Well this was the question and the let us assume a result (potentially true upon the basis of primality though)

I wouldn't long divide. Just saying you might have.I thought you were the one that hated long division
Though yeah that never crosses my mind with algebra anymore unless I explicitly see polynomials
If your gcd != 1 and your desired number in this case being 8 is not equal to the gcd then you divide everything by the gcd(including the modulus) and multiply everything by 8 except the modulus.The question isn't hard but I just want to see it get done because I want to see how you'd set out your working
I'll put down the relevant Euclidean algorithm to save a bit of work
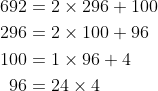
nek minute fails...Woohoo no more first year math again
Shoutout to everyone who helped esp InteGrand
Can you like, not jinx it plesnek minute fails...
Thanks integrand you've saved my wam

