Discrete Maths Last Minute questions (3 Viewers)

InteGrand · Nov 13, 2016

Drsoccerball said:
$B \cup B^c \subseteq C$

$U \subseteq C$

$\therefore C = U$

How did you get U being a subset of C? (It would be the other way around in general.)

Drsoccerball · Nov 13, 2016

InteGrand said:
How did you get U being a subset of C? (It would be the other way around in general.)

Because we have:

$B^c \subseteq C $ and $ B \subseteq C $ If either of these weren't true then we would already have $ A \subseteq C.$

InteGrand · Nov 13, 2016

Drsoccerball said:
Because we have:

$B^c \subseteq C $ and $ B \subseteq C $ If either of these weren't true then we would already have $ A \subseteq C.$

Ah right yeah, didn't read it carefully before. But I think your earlier steps are dodgy or strangely worded. Here's a way to do it.

Assume the hypotheses about A,B,C and let x be in A. If x is also in B, then x is in A∩B, which implies it's in C (since A∩B ⊆ C). If x is not in B, then x is in A – B, which implies it's in C (as A – B ⊆ C). Hence either way, x is in C, whence A ⊆ C.

Drsoccerball · Nov 13, 2016

InteGrand said:
Ah right yeah, didn't read it carefully before. But I think your earlier steps are dodgy or strangely worded. Here's a way to do it.

Assume the hypotheses about A,B,C and let x be in A. If x is also in B, then x is in A∩B, which implies it's in C (since A∩B ⊆ C). If x is not in B, then x is in A – B, which implies it's in C (as A – B ⊆ C). Hence either way, x is in C, whence A ⊆ C.

That's much more straightfoward. But I still think my way is perfectly valid can't see anything wrong with it

Thanks

InteGrand · Nov 13, 2016

Drsoccerball said:
That's much more straightfoward. But I still think my way is perfectly valid can't see anything wrong with it
Thanks

Possibly your intentions may have been valid, but I'm not exactly sure what you meant by your wordings. Like what did you mean when you wrote for example "Either x ∈ A ⟺ x ∈ C" near the beginning? Note also that C doesn't have to be the universal set, but it turns out that C just has to be a superset of (i.e. have as a subset) A (which is what we needed to prove). E.g. if A = {1, 2}, B = {2, 3}, and C = {1, 2, 3, 4}, then A \ B = {1} ⊆ C and A∩B = {2} ⊆ C, but it need not be that C be the universal set (since the universal set may be the set of all positive integers for example). It wouldn't then hold that B^c ⊆ C.

Drsoccerball · Nov 13, 2016

If x is and element of A then x is also an element of C (a is a subset of C). I think instead of writing "or" I should've wrote "and" as it is an intersection. So the last step is not required and the proof pretty much is your proof. (Just got confused with and/or).

Edit: If it was union instead of intersection I think the last step I did would be required right?

InteGrand · Nov 13, 2016

Drsoccerball said:
If x is and element of A then x is also an element of C

To say this with an arrow, we should use an arrow like this: ⇒. This arrow means "if ... then" (i.e. "implies"). The one you used (double-sided arrow) instead means "if and only if" (makes sense, since that arrow goes both ways).

Drsoccerball · Nov 13, 2016

InteGrand said:
To say this with an arrow, we should use an arrow like this: ⇒. This arrow means "if ... then" (i.e. "implies"). The one you used (double-sided arrow) instead means "if and only if" (makes sense, since that arrow goes both ways).

I was more trying to say this implies is that the same thing?

InteGrand · Nov 13, 2016

Drsoccerball said:
I was more trying to say this implies is that the same thing?

"Implies" is the "if...then" (these two are the same thing) and should be written with a "⇒" arrow if you use an arrow.

"If and only if" is different (as it goes in both directions) and is denoted with an "⟺" arrow.

The "⟺" arrow can't be used for "implies", and the "⇒" arrow can't be used to mean if and only if. (Because these are two very different things.)

leehuan · Nov 14, 2016

Suppose that 26 integers are chosen from the set S={1, 2, ..., 50}

By writing these numbers as 2^km with m odd, prove that one of the chosen numbers is a multiple of another of the chosen numbers.

InteGrand · Nov 14, 2016

leehuan said:
Suppose that 26 integers are chosen from the set S={1, 2, ..., 50}

By writing these numbers as 2^km with m odd, prove that one of the chosen numbers is a multiple of another of the chosen numbers.

$\noindent To get started: numbers $1,2,4,\ldots 32$ are $2^{k}\cdot 1$, $k=0,1,\ldots,5$. With $m=3$, they are $3,6,12,\ldots, 48$, i.e. $2^{k}\cdot 3$, for $k = 0,1,2,3, 4$. With $m=5$, they are $5,10,20,40$, i.e. $2^{k}\cdot 5$, with $k=0,1,2,3$. The next bunch is $2^{k}\cdot 7$, with $k = 0,1,2$. Can you spot and prove a pattern and use it to prove a desired result?$

leehuan · Nov 14, 2016

InteGrand said:
$\noindent To get started: numbers $1,2,4,\ldots 32$ are $2^{k}\cdot 1$, $k=0,1,\ldots,5$. With $m=3$, they are $3,6,12,\ldots, 48$, i.e. $2^{k}\cdot 3$, for $k = 0,1,2,3, 4$. With $m=5$, they are $5,10,20,40$, i.e. $2^{k}\cdot 5$, with $k=0,1,2,3$. The next bunch is $2^{k}\cdot 7$, with $k = 0,1,2$. Can you spot and prove a pattern and use it to prove a desired result?$

Hmm interesting, the values of k are going down.

But the more obvious pattern of k going down by 1 seems to halt...

$\text{Wait a minute. Are our holes:}\\ S_1=\{2^k(1)\}\\ S_3=\{2^k(3)\}\\ \vdots\\ S_{25}=\{2^k(25)\}$

Drsoccerball · Nov 14, 2016

InteGrand said:
$\noindent To get started: numbers $1,2,4,\ldots 32$ are $2^{k}\cdot 1$, $k=0,1,\ldots,5$. With $m=3$, they are $3,6,12,\ldots, 48$, i.e. $2^{k}\cdot 3$, for $k = 0,1,2,3, 4$. With $m=5$, they are $5,10,20,40$, i.e. $2^{k}\cdot 5$, with $k=0,1,2,3$. The next bunch is $2^{k}\cdot 7$, with $k = 0,1,2$. Can you spot and prove a pattern and use it to prove a desired result?$

The way I did it was that the worst case scenario is when we pick {26,27,...,50} since none are multiples of the other and by the pigeon hole principle we have to pick another number which is a multiple of one of the other numbers already picked.

InteGrand · Nov 14, 2016

leehuan said:
Hmm interesting, the values of k are going down.

But the more obvious pattern of k going down by 1 seems to halt...

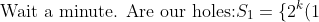$\text{Wait a minute. Are our holes:}\\ S_1=\{2^k(1)\}\\ S_3=\{2^k(3)\}\\ \vdots\\ S_{25}=\{2^k(25)\}$

$\noindent Almost, but these miss out on the odd numbers bigger than $\frac{50}{2} = 25$. These odd numbers $27,29,31,\ldots, 49$ (there are $\color{blue}{12}$ of them) each have just themselves in their set $S_{m}$. So the sets you wrote $S_{1}, S_{3}, S_{5},\ldots, S_{25}$ (there are $\color{red}{13}$ such, each with at least two elements), together with the singleton sets $S_{27},S_{29},\ldots, S_{49}$ will partition the set $S$ (exercise). Since we are picking $26$ elements and there are $\color{blue}{12}\color{black}{+} \color{red}{13}\color{black} = 25$ subsets $S_{m}$, there'll be a set $S_{m}$ with two elements picked out of it (which'll come from the ones before or at $m=25$, since these are the only ones with at least two members). In this set, we'll have two numbers we picked that has one a multiple of the other.$

leehuan · Nov 14, 2016

Consider the 10 letter word PARRAMATTA and all the words formed by rearranging its letters. How many of these words contain the subword MAP but not the subword RAT?

They gave no answer so I'm asking for checking:

$8 \times \frac{7!}{3!2!2!}+ 6\times5\times \frac{4!}{2!}$

Drsoccerball · Nov 14, 2016

leehuan said:
Consider the 10 letter word PARRAMATTA and all the words formed by rearranging its letters. How many of these words contain the subword MAP but not the subword RAT?

They gave no answer so I'm asking for checking:

$8 \times \frac{7!}{3!2!2!}+ 6\times5\times \frac{4!}{2!}$

What I did was :

Words which contain map - words which containt map and rat (Also take note that rat can appear twice) + missing

leehuan · Nov 14, 2016

Drsoccerball said:
What I did was :

Words which contain map - words which containt map and rat (Also take note that rat can appear twice) + missing

Good observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/excl

Drsoccerball · Nov 14, 2016

leehuan said:
Good observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/excl

Its funny because I only picked that up when writing my though pattern lel... Need help for the exam

leehuan · Nov 14, 2016

In that case, I now have

$8\times\frac{7!}{3!2!2!}-\left(6\times5\times\frac{4!}{2!}-\frac{4!}{2!}\right)$

Drsoccerball · Nov 14, 2016

leehuan said:
Good observation. Also in my working that + should've been a minus but I need to do redo the whole thing anyway cause of the incl/excl

Just to compare answers I got : $\frac{8!}{3!2!2!} - \frac{6!}{2!} +4! .$

Discrete Maths Last Minute questions (3 Viewers)

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 3)