-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Continuous random variables (1 Viewer)
- Thread starter leehuan
- Start date
The time between Poisson events follows an exponential distribution.What even is this exponential distribution question getting at?
(This was Q39 - a Poisson discrete R.V. question)
 Find the probability of getting at least one "once in a hundred year" flood in a 100 year period.$)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Yeah the analogy does make sense if I process it, but then I still can't apply it to this question because I have no clue where my parameters go
And I have a feeling I'm trying to integrate to find) but that definitely doesn't look right
but that definitely doesn't look right
Edit: ...Oh crap wait was I meant to find) ...
...
(Final answer is e-0.5)
And I have a feeling I'm trying to integrate to find
Edit: ...Oh crap wait was I meant to find
(Final answer is e-0.5)
Yeah the analogy does make sense if I process it, but then I still can't apply it to this question because I have no clue where my parameters go
And I have a feeling I'm trying to integrate to findbut that definitely doesn't look right
Edit: ...Oh crap wait was I meant to find...
(Final answer is e-0.5)
I can't see the initial Q., but this lambda is the same lambda as the Poisson one, provided that the time units are the same.
Last edited:
- Joined
- Feb 16, 2005
- Messages
- 8,386
- Gender
- Male
- HSC
- 2006
Use the substitutionWhat am I even trying to integrate.
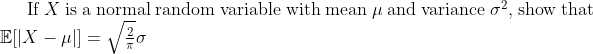
and the result follows
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Whoops. Should've checked my notes; seems I got my expected value formula wrong.Use the substitutionnoting that
and the result follows
The payoff P is 0 if and only if 50 – X ≤ 0, i.e. iff X ≥ 50. So find Pr(X ≥ 50) (this'll be the answer).
(Ans is 0.0062 but I'm happy for just the question to be broken down - no need to do the standardisation process and etc. for me)
The reason is that P = max(50 – X, 0). So for P to be 0, we need and want the maximum of those two to be 0. This'll happen if and only if the 50 – X is 0 or less.
Last edited:
I've got no idea what to do either of these statements
^2}dx=\int_0^\infty \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{u-\mu}{\sigma}\right)^2}e^udu)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Getting lost between my Poisson<->exponential again
The probability distribution of the number of claims you will have in a year is Poisson(0.1). Determine the expected time to the next claim and the probability that you will have a claim in the next 18 months.
I thought that the time till next claim will follow Exp(10), but this implies that the expected time is 0.1 which is wrong. Where did my reasoning go flawed?
The probability distribution of the number of claims you will have in a year is Poisson(0.1). Determine the expected time to the next claim and the probability that you will have a claim in the next 18 months.
I thought that the time till next claim will follow Exp(10), but this implies that the expected time is 0.1 which is wrong. Where did my reasoning go flawed?
The expected time to the next claim is 10 years (inverse of the rate parameter in the Poisson distribution). Depending on which convention of the Exponential you're using, the time to next claim is either Exp(10) or Exp(0.1).Getting lost between my Poisson<->exponential again
The probability distribution of the number of claims you will have in a year is Poisson(0.1). Determine the expected time to the next claim and the probability that you will have a claim in the next 18 months.
I thought that the time till next claim will follow Exp(10), but this implies that the expected time is 0.1 which is wrong. Where did my reasoning go flawed?
I think you may have been confused between the two conventions, because on the one hand you said it's Exp(10), but on the other hand you said the mean of an Exp(10) is 1/10.
If you're using the convention where Exp(something) refers to a mean of 1/something ("something" being the parameter), then the rule would be: "If X ~ Poisson(lambda), then T ~ Exp(lambda)" (where T is the time between two Poisson events r.v.).
So using that convention of Exp, since we're told X ~ Poisson(0.1) (X being no. of claims per year), it means T ~ Exp(0.1), and E[T] = 1/(0.1) = 10.
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Ah so there are actually two conventions in which it's described. Fair enough.The expected time to the next claim is 10 years (inverse of the rate parameter in the Poisson distribution). Depending on which convention of the Exponential you're using, the time to next claim is either Exp(10) or Exp(0.1).
Pretty annoying though; it wrecked my brain a bit. Anyone know why there happened to be two conventions?
Just depending on the situation, one may be more natural than the other.Ah so there are actually two conventions in which it's described. Fair enough.
Pretty annoying though; it wrecked my brain a bit. Anyone know why there happened to be two conventions?
(I just numbered the two Conventions here myself, I'm not saying that they're universally referred to as Convention 1 and 2.)
Basically, if you think of these things in terms of the rate parameter and the MTBF (mean time between failures), you'll be less likely to make a mistake. The conventions are really just notational things, but the rate parameter and the MTBF will be intrinsic to the system in question.
So if you think of it as "E[T] = inverse of rate parameter = MTBF parameter" and "Var[T] = (inverse of rate parameter)^2 = (MTBF)^2", etc., you'll be less likely to slip up than if you think of it as "Exp(lambda) has mean lambda" (because the latter part requires you to remember notation/convention whereas the former is independent of which convention or notation is used).
E.g. if we're told X ~ Poisson(7), that tells us the "rate parameter" of the Poisson process is 7 (because Poisson only has one convention, so no confusions with this), so then we know T has mean 1/7 (= 1/(rate parameter)), and we also know the pdf of T is 7e-7t (because we are remembering the pdf as "rate parameter * exp(-(rate parameter)*t)).
Similarly, if we're told T is the lifetime of a lightbulb that has expected lifetime 500 hours and is exponentially distributed, we know that the pdf is (1/500)*exp(-(t/500)), because we are remembering the pdf as being "1/(MTBF) * exp(-(t/MTBF))". If we instead just remembered it via the notation method, we could get confused between the two conventions (because we'd need to be sure about whether it's Exp(500), or Exp(1/500), etc.).
[You should still know the conventions though, of course, but just make sure to also understand these in terms of rate parameter and MTBF so that you can get the right answers etc.]
So if you think of it as "E[T] = inverse of rate parameter = MTBF parameter" and "Var[T] = (inverse of rate parameter)^2 = (MTBF)^2", etc., you'll be less likely to slip up than if you think of it as "Exp(lambda) has mean lambda" (because the latter part requires you to remember notation/convention whereas the former is independent of which convention or notation is used).
E.g. if we're told X ~ Poisson(7), that tells us the "rate parameter" of the Poisson process is 7 (because Poisson only has one convention, so no confusions with this), so then we know T has mean 1/7 (= 1/(rate parameter)), and we also know the pdf of T is 7e-7t (because we are remembering the pdf as "rate parameter * exp(-(rate parameter)*t)).
Similarly, if we're told T is the lifetime of a lightbulb that has expected lifetime 500 hours and is exponentially distributed, we know that the pdf is (1/500)*exp(-(t/500)), because we are remembering the pdf as being "1/(MTBF) * exp(-(t/MTBF))". If we instead just remembered it via the notation method, we could get confused between the two conventions (because we'd need to be sure about whether it's Exp(500), or Exp(1/500), etc.).
[You should still know the conventions though, of course, but just make sure to also understand these in terms of rate parameter and MTBF so that you can get the right answers etc.]
Last edited:

