Continuous random variables (1 Viewer)

leehuan · May 22, 2016

What even is this exponential distribution question getting at?

$Q: For the situation of Exercise 39 find the probability of there being a 50 year gap between 'once in a hundred years' floods$

(This was Q39 - a Poisson discrete R.V. question)
$The number of 'once in a hundred years' floods can be modelled by a Poisson distribution. \\ a) Find the probability of getting at least one 'once in a hundred year' flood in a 100 year period.$

InteGrand · May 22, 2016

leehuan said:
What even is this exponential distribution question getting at?

$Q: For the situation of Exercise 39 find the probability of there being a 50 year gap between "once in a hundred years" floods$

(This was Q39 - a Poisson discrete R.V. question)
$The number of 'once in a hundred years' floods can be modelled by a Poisson distribution. \\ a) Find the probability of getting at least one "once in a hundred year" flood in a 100 year period.$

The time between Poisson events follows an exponential distribution.

$\noindent If $X \sim \mathrm{Poisson}\left(\lambda\right)$, and $T$ is the time between two (consecutive) of these Poisson events, then $T\sim \mathrm{Exponential}\left(\lambda\right)$, with pdf $f_{T} \left(t\right) = \lambda e^{-\lambda t}$, for $t>0$. The mean time between events here is $\mathbb{E}\left[T\right] = \frac{1}{\lambda}$.$

$\noindent The significance of $\lambda$ is that it is the mean number of the Poisson events per unit time.$

leehuan · May 22, 2016

Yeah the analogy does make sense if I process it, but then I still can't apply it to this question because I have no clue where my parameters go

And I have a feeling I'm trying to integrate to find $P(t_1 \le T \le t_1+50)$ but that definitely doesn't look right

Edit: ...Oh crap wait was I meant to find $P(T \ge 50)$ ...

(Final answer is e^-0.5)

InteGrand · May 22, 2016

leehuan said:
Yeah the analogy does make sense if I process it, but then I still can't apply it to this question because I have no clue where my parameters go

And I have a feeling I'm trying to integrate to find $P(t_1 \le T \le t_1+50)$ but that definitely doesn't look right

Edit: ...Oh crap wait was I meant to find $P(T \ge 50)$ ...

(Final answer is e^-0.5)

$\noindent Note that the CDF of an $\mathrm{Exp}\left(\lambda\right)$ random variable is $F_{T} (t) = 1-e^{-\lambda t}$, for $t>0$. So the complementary CDF is $\overline{F}_{T}\left(t\right)=e^{-\lambda t}$ (probability of $T$ being greater than a given $t$).$

I can't see the initial Q., but this lambda is the same lambda as the Poisson one, provided that the time units are the same.

leehuan · May 22, 2016

This one has been doing my head in.

$Suppose $X$ is a continuous random variable with probability density $f$, and $\phi$ is a continuous increasing differentiable function.$

$$a) Show that the probability density $g$ of $Y=\phi (X)$ is given by$\\ g(y)=f(\phi^{-1}(y)) \cdot \frac{d}{dy} \phi^{-1}(y)$

$$b) Show that the expected value of Y is$ \\ \mathbb E [Y] = \int_{ -\infty}^{\infty}{\phi(x)f(x)dx}$

InteGrand · May 22, 2016

leehuan said:
This one has been doing my head in.

$Suppose $X$ is a continuous random variable with probability density $f$, and $\phi$ is a continuous increasing differentiable function.$

$$a) Show that the probability density $g$ of $Y=\phi (X)$ is given by$\\ g(y)=f(\phi^{-1}(y)) \cdot \frac{d}{dy} \phi^{-1}(y)$

$$b) Show that the expected value of Y is$ \\ \mathbb E [Y] = \int_{ -\infty}^{\infty}{\phi(x)f(x)dx}$

$\noindent a) We have$

$\begin{align*}F_{Y} \left(y\right) &= \mathbb{P}\left(Y \leq y\right) \\ &= \mathbb{P}\left(\phi\left(X\right) \leq y\right) \\ &= \mathbb{P}\left(X \leq \phi ^{-1} \left(y\right) \right) \quad (\text{as }\phi \text{ is increasing}) \\ &= F_{X}\left( \phi ^{-1} \left(y\right)\right). \end{align*}$

$\noindent Differentiating wrt $y$ and using the chain rule shows that $f_{Y} \left(y\right) = f_{X}\left( \phi ^{-1} \left(y\right)\right)\cdot \frac{\mathrm{d}}{\mathrm{d}y}\left(\phi ^{-1} \left(y\right)\right)$, as required.$

$\noindent b) Note that we have $\mathbb{E}\left[Y\right] = \int _{-\infty}^{\infty}y f_{Y} \left(y\right) \text{ d}y = \int _{-\infty}^{\infty}y f_{X}\left( \phi ^{-1} \left(y\right)\right)\cdot \frac{\mathrm{d}}{\mathrm{d}y}\left(\phi ^{-1} \left(y\right)\right)\text{ d}y$. Make the substitution $y=\phi (x)\Longleftrightarrow x =\phi ^{-1} \left(y\right)$. So $\mathrm{d}x= \frac{\mathrm{d}}{\mathrm{d}y}\left(\phi ^{-1} \left(y\right)\right)\text{ d}y$. Hence$

$\begin{align*}\mathbb{E}\left[Y\right] &= \int _{-\infty}^{\infty}\phi (x) f_{X} (x) \text{ d}x.\end{align*}$

$\noindent The limits of the integrals need only be taken over the places where the pdf's are positive (these sets being called the `support' of the random variable). By taking them over the whole real line, we simply have the density being $0$ at other places and the integrals' values are still the same then.$

leehuan · May 29, 2016

What am I even trying to integrate.

$$If $X$ is a normal random variable with mean $\mu$ and variance $\sigma^2$, show that \\ $\mathbb E [|X-\mu |]=\sqrt{\frac{2}{\pi}}\sigma$

Trebla · May 29, 2016

leehuan said:
What am I even trying to integrate.

$$If $X$ is a normal random variable with mean $\mu$ and variance $\sigma^2$, show that \\ $\mathbb E [|X-\mu |]=\sqrt{\frac{2}{\pi}}\sigma$

Use the substitution $z=\dfrac{x-\mu}{\sigma}$ noting that $\sigma>0$

$E|X-\mu|=\dfrac{1}{\sigma\sqrt{2\pi}}\displaystyle\int_{-\infty}^{\infty}|x-\mu|e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\,dx\\\\ = \dfrac{\sigma}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{\infty}|z|e^{-\frac{1}{2}z^2}\,dz\\\\ = \dfrac{2\sigma}{\sqrt{2\pi}}\displaystyle\int_0^{ \infty}ze^{-\frac{1}{2}z^2}\,dz$

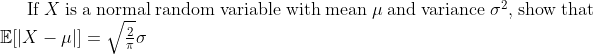
and the result follows

leehuan · May 29, 2016

Trebla said:
Use the substitution $z=\dfrac{x-\mu}{\sigma}$ noting that $\sigma>0$

$E|X-\mu|=\dfrac{1}{\sigma\sqrt{2\pi}}\displaystyle\int_{-\infty}^{\infty}|x-\mu|e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\,dx\\\\ = \dfrac{\sigma}{\sqrt{2\pi}}\displaystyle\int_{-\infty}^{\infty}|z|e^{-\frac{1}{2}z^2}\,dz\\\\ = \dfrac{2\sigma}{\sqrt{2\pi}}\displaystyle\int_0^{ \infty}ze^{-\frac{1}{2}z^2}\,dz$

and the result follows

Whoops. Should've checked my notes; seems I got my expected value formula wrong.

leehuan · Jun 3, 2016

$Let $X$ be a random variable modelling the value of an asset at a fixed time $T$ in the future. The payoff for a put option with strike $ \$50 $at time $T$ is given by$ \\ P = \max (50-X,0)\\ $If $X$ is normally distributed with mean 40 and variance 16, estimate the probability the payoff is zero.$

(Ans is 0.0062 but I'm happy for just the question to be broken down - no need to do the standardisation process and etc. for me)

InteGrand · Jun 4, 2016

leehuan said:
$Let $X$ be a random variable modelling the value of an asset at a fixed time $T$ in the future. The payoff for a put option with strike $ \$50 $at time $T$ is given by$ \\ P = \max (50-X,0)\\ $If $X$ is normally distributed with mean 40 and variance 16, estimate the probability the payoff is zero.$

(Ans is 0.0062 but I'm happy for just the question to be broken down - no need to do the standardisation process and etc. for me)

The payoff P is 0 if and only if 50 – X ≤ 0, i.e. iff X ≥ 50. So find Pr(X ≥ 50) (this'll be the answer).

The reason is that P = max(50 – X, 0). So for P to be 0, we need and want the maximum of those two to be 0. This'll happen if and only if the 50 – X is 0 or less.

leehuan · Aug 6, 2016

$$Prove that the expectation for the log-normal distribution is $\\\mathbb{E}[X]=e^{\mu + \frac{1}{2}\sigma^2}$

I've got no idea what to do either of these statements
$\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{\ln x - \mu}{\sigma}\right)^2}dx=\int_0^\infty \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{u-\mu}{\sigma}\right)^2}e^udu$

InteGrand · Aug 6, 2016

leehuan said:
$$Prove that the expectation for the log-normal distribution is $\\\mathbb{E}[X]=e^{\mu + \frac{1}{2}\sigma^2}$

I've got no idea what to do either of these statements
$\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{\ln x - \mu}{\sigma}\right)^2}dx=\int_0^\infty \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{u-\mu}{\sigma}\right)^2}e^udu$

$\noindent Note if $X$ is log-normal with parameters $\mu, \sigma^2$, ($\sigma >0$) then the PDF is $f(x) = \frac{1}{\sqrt{2\pi}\sigma x} \exp \left(-\frac{1}{2} \left(\frac{\ln x -\mu }{\sigma}\right)^2\right)$, for $x >0$. Then $\mathbb{E}\left[X\right] =\int _0 ^\infty xf(x)\, \mathrm{d}x$. To calculate this integral, make a substitution like $z =\frac{\ln x -\mu}{\sigma}$, and remember to change the limits (they'll become from $-\infty$ to $\infty$). Also note $\mathrm{d}z = \frac{1}{\sigma x}\, \mathrm{d}x$. Make sure to recall the Gaussian integral when needed, and use the technique of \textsl{completing the square} in the exponent to get it into the Gaussian integral shape.$

leehuan · Oct 3, 2016

Getting lost between my Poisson<->exponential again

The probability distribution of the number of claims you will have in a year is Poisson(0.1). Determine the expected time to the next claim and the probability that you will have a claim in the next 18 months.

I thought that the time till next claim will follow Exp(10), but this implies that the expected time is 0.1 which is wrong. Where did my reasoning go flawed?

InteGrand · Oct 3, 2016

leehuan said:
Getting lost between my Poisson<->exponential again

The probability distribution of the number of claims you will have in a year is Poisson(0.1). Determine the expected time to the next claim and the probability that you will have a claim in the next 18 months.

I thought that the time till next claim will follow Exp(10), but this implies that the expected time is 0.1 which is wrong. Where did my reasoning go flawed?

The expected time to the next claim is 10 years (inverse of the rate parameter in the Poisson distribution). Depending on which convention of the Exponential you're using, the time to next claim is either Exp(10) or Exp(0.1).

I think you may have been confused between the two conventions, because on the one hand you said it's Exp(10), but on the other hand you said the mean of an Exp(10) is 1/10.

If you're using the convention where Exp(something) refers to a mean of 1/something ("something" being the parameter), then the rule would be: "If X ~ Poisson(lambda), then T ~ Exp(lambda)" (where T is the time between two Poisson events r.v.).

So using that convention of Exp, since we're told X ~ Poisson(0.1) (X being no. of claims per year), it means T ~ Exp(0.1), and E[T] = 1/(0.1) = 10.

leehuan · Oct 3, 2016

InteGrand said:
The expected time to the next claim is 10 years (inverse of the rate parameter in the Poisson distribution). Depending on which convention of the Exponential you're using, the time to next claim is either Exp(10) or Exp(0.1).

Ah so there are actually two conventions in which it's described. Fair enough.

Pretty annoying though; it wrecked my brain a bit. Anyone know why there happened to be two conventions?

InteGrand · Oct 3, 2016

leehuan said:
Ah so there are actually two conventions in which it's described. Fair enough.

Pretty annoying though; it wrecked my brain a bit. Anyone know why there happened to be two conventions?

Just depending on the situation, one may be more natural than the other.

$\noindent Convention 1: $T \sim \mathrm{Exp}(\lambda)$ means pdf is $f_{T} (t) = \lambda e^{-\lambda t}$ (for $t > 0$). In this convention, $\lambda$ is the ``rate'' of occurrence of the underlying Poisson process (e.g. $0.1$ per year in the claims example, which is clearly a rate). So this convention may be more natural if we're doing things in terms of a given rate.$

$\noindent Convention 2: $T\sim \mathrm{Exp}(\beta)$ refers to the pdf being $f_{T} (t) = \frac{1}{\beta}e^{- \frac{t}{\beta}}$, $t >0$. In this convention, the significance of $\beta$ is that it is the \emph{mean time between failures} (i.e. mean time between occurrences of the underlying Poisson process. Commonly called failures because exponential distribution (and related ones) often model the time till something fails, like time till a lightbulb dies or something).$

$\noindent Convention 2 may be more natural if we're dealing with things in terms of their mean lifetimes, or if what we're interested in is moreso the mean lifetimes than the ``rate''. E.g. if we're told a lightbulb has mean lifetime $1000$ hours and its lifetime $T$ is exponentially distributed, then it may be more natural to talk about it as $T\sim \mathrm{Exp}\left(1000\right)$, so we can easily see what the the mean time between failures is.$

$\noindent For your convenience, under Convention 1: if $T\sim \mathrm{Exp}(\lambda)$, then $\mathbb{E}[T] = \frac{1}{\lambda}$, $\mathrm{Var}[T] = \frac{1}{\lambda^{2}}$, where $\lambda$ is the parameter, which is a \emph{rate parameter}, and satisfies $\lambda = \beta^{-1}$, where $\beta$ is the mean time between failures for the process.$

$\noindent Under Convention 2: if $T \sim \mathrm{Exp}(\beta)$, then $\mathbb{E}[T] = \beta$, and $\mathrm{Var}[T] = \beta^{2}$, where $\beta$ is the \emph{mean time between failures}, and $\beta = \lambda^{-1}$, where $\lambda$ is the rate parameter of the underlying Poisson process.$

$\noindent In general to convert between any formulas involved in the two conventions for a given system, just use the relation $\lambda = \beta^{-1} \iff \beta = \lambda^{-1}$.$

(I just numbered the two Conventions here myself, I'm not saying that they're universally referred to as Convention 1 and 2.)

InteGrand · Oct 3, 2016

Basically, if you think of these things in terms of the rate parameter and the MTBF (mean time between failures), you'll be less likely to make a mistake. The conventions are really just notational things, but the rate parameter and the MTBF will be intrinsic to the system in question.

So if you think of it as "E[T] = inverse of rate parameter = MTBF parameter" and "Var[T] = (inverse of rate parameter)^2 = (MTBF)^2", etc., you'll be less likely to slip up than if you think of it as "Exp(lambda) has mean lambda" (because the latter part requires you to remember notation/convention whereas the former is independent of which convention or notation is used).

E.g. if we're told X ~ Poisson(7), that tells us the "rate parameter" of the Poisson process is 7 (because Poisson only has one convention, so no confusions with this), so then we know T has mean 1/7 (= 1/(rate parameter)), and we also know the pdf of T is 7e^-7t (because we are remembering the pdf as "rate parameter * exp(-(rate parameter)*t)).

Similarly, if we're told T is the lifetime of a lightbulb that has expected lifetime 500 hours and is exponentially distributed, we know that the pdf is (1/500)*exp(-(t/500)), because we are remembering the pdf as being "1/(MTBF) * exp(-(t/MTBF))". If we instead just remembered it via the notation method, we could get confused between the two conventions (because we'd need to be sure about whether it's Exp(500), or Exp(1/500), etc.).

[You should still know the conventions though, of course, but just make sure to also understand these in terms of rate parameter and MTBF so that you can get the right answers etc.]

Continuous random variables (1 Viewer)

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

Trebla

Administrator

leehuan

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

leehuan

Well-Known Member

InteGrand

Well-Known Member

InteGrand

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)