-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Improper integrals (1 Viewer)
- Thread starter leehuan
- Start date
The Cauchy principal value would be 0. Otherwise it's an undefined expression -inf + inf.
The answer is obviously that it does not, but I want to check if my proof is flawed.
I have a feeling I may have needed to consider the negative infinity portion of this integral?
Don't need to use any comparison tests, we can find an antiderivative using inspection or a u-substitution.
Last edited:
Paradoxica
-insert title here-
Does it make sense to ask convergence of an integral whose CPV is 0?
The answer is obviously that it does not, but I want to check if my proof is flawed.
I have a feeling I may have needed to consider the negative infinity portion of this integral?
In any case, you can reduce the two cases to one by using the parity of the function to your advantage.
Paradoxica
-insert title here-
yeah, that's just the CPV.They didn't teach us about the Cauchy principal value. I only found that on WolframAlpha.
Edit: Though they did make us evaluate this
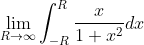
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
I suppose the question was just meant to distinguish between the two. But like I said, our course makes no reference to CPV.yeah, that's just the CPV.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
My bad. Question still holds out of my fatigue though please?Typo? 'a' is 'p'?
It ends up just being the p-test when you do a change of variables (substitute u = ln(x)).Bit of guidance needed here.
}^{p}}}$ converges.$)
So it converges iff p > 1.
The -t in the exponential should become -1/x , rather than 1/x.
(I know this is the Gamma function)
I had an idea but then I got lost. My last step was rewriting the integral as
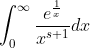
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
So you have the integrand 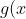=x^{-1-s}e^{-x^{-1}}) and we want to show it is integrable on the non-negative reals.
and we want to show it is integrable on the non-negative reals.
The behaviour near zero is not a problem at all, since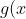\rightarrow 0) as
as 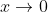 (essentially because exponentials dominate polynomials, there are many ways you could justify this). So it suffices to check that g be integrable on
(essentially because exponentials dominate polynomials, there are many ways you could justify this). So it suffices to check that g be integrable on ) .
.
This follows by comparison to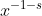 . (In fact we can use this argument to show that the integral is convergent if and ONLY if
. (In fact we can use this argument to show that the integral is convergent if and ONLY if 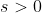 ).
).
The behaviour near zero is not a problem at all, since
This follows by comparison to
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Mistake in typing, my badThe -t in the exponential should become -1/x , rather than 1/x.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Having already shown 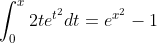
e^{t^2}dt}\to \infty$ as $x \to \infty)
The method the answers provided is not immediately obvious to me and I don't understand the lateral thinking required. Can someone please explain the intuition required to see this method or just provide an easier pathway?
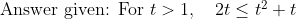
e^{t^2}dt}&=\int_0^1{\left(t^2+t\right)e^{t^2}dt}+\int_1^x{ \left( t^2+t \right) e^{t^2}dt}\\ & \ge \int_0^1{\left(t^2+t\right)e^{t^2}dt} + \int_1^x{2te^{t^2}dt} \\ &= \int_0^1{\left(t^2-t\right)e^{t^2}dt} + \int_0^x{2te^{t^2}dt}\\ &= \int_0^1{\left(t^2-t\right)e^{t^2}dt} + e^{x^2}-1 \to \infty \end{align*})
The method the answers provided is not immediately obvious to me and I don't understand the lateral thinking required. Can someone please explain the intuition required to see this method or just provide an easier pathway?
Yeah it's essentially a comparison test.Having already shown
The method the answers provided is not immediately obvious to me and I don't understand the lateral thinking required. Can someone please explain the intuition required to see this method or just provide an easier pathway?
e^{t^2}dt}&=\int_0^1{\left(t^2+t\right)e^{t^2}dt}+\int_1^x{ \left( t^2+t \right) e^{t^2}dt}\\ & \ge \int_0^1{\left(t^2+t\right)e^{t^2}dt} + \int_1^x{2te^{t^2}dt} \\ &= \int_0^1{\left(t^2-t\right)e^{t^2}dt} + \int_0^x{2te^{t^2}dt}\\ &= \int_0^1{\left(t^2-t\right)e^{t^2}dt} + e^{x^2}-1 \to \infty \end{align*})
For all t large enough, the integrand in the second integral is greater than the first (since t^2 + t > 2t for all t large enough, say all t > 1).
Since the former integral taken from 1 to oo diverges to +oo (from previous part of Q.), by the comparison test, so does the latter one when taken from 1 to oo.
And remembering the finite lower limit here is irrelevant since the integrand is continuous, we're done.

