Last edited:
-
Interested in being a marker for this year's BoS Maths Trials? Let us know before 31 August, see this thread for details
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Marathon (archive) (1 Viewer)
- Thread starter Trebla
- Start date
- Status
- Not open for further replies.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Zlatman
Member
- Joined
- Nov 4, 2014
- Messages
- 73
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
For this one, we just need the following equations:
 (i.e. horizontal component of tension (LHS) provides centripetal force (RHS))
(i.e. horizontal component of tension (LHS) provides centripetal force (RHS))
 (weight force (RHS) equal in magnitude to vertical component of tension force (LHS) due to no acceleration in vertical direction).
(weight force (RHS) equal in magnitude to vertical component of tension force (LHS) due to no acceleration in vertical direction).
where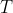 is the magnitude of the maximal tension force and m and ω are as given in my previous post. The only unknowns in these simultaneous equations are T and θ, and we just need to solve for T to get the answer.
is the magnitude of the maximal tension force and m and ω are as given in my previous post. The only unknowns in these simultaneous equations are T and θ, and we just need to solve for T to get the answer.
Edit: and as we can see, only the first equation is needed to find T. Just cancel cos(θ)'s. This is the derivation of the formula (which I never memorised but which I think is in textbooks).
(which I never memorised but which I think is in textbooks).
That formula is irrelevant for this one. That formula refers to the period T of particle's circular motion (time to complete one revolution) if its angular velocity is w, but we don't need that now.umm... where does this formula come in
For this one, we just need the following equations:
where
Edit: and as we can see, only the first equation is needed to find T. Just cancel cos(θ)'s. This is the derivation of the formula
Last edited:
asdfghjklqwerty
Member
- Joined
- Sep 14, 2015
- Messages
- 33
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
what i did was T=Mw^2r
and w= (45x 2pi)/60
and the rest is ezpz
what i did was T=Mw^2r
and w= (45x 2pi)/60
and the rest is ezpz
Re: HSC 2015 4U Marathon
 , since 'r' normally refers to the radius.
, since 'r' normally refers to the radius.
By 'r', you mean the string length (3 m), not the radius, right? Probably better to writewhat i did was T=Mw^2r
and w= (45x 2pi)/60
and the rest is ezpz
Paradoxica
-insert title here-
Re: HSC 2015 4U Marathon

There is a very easy way to do this.
There is a very easy way to do this.
Re: HSC 2015 4U Marathon
Edit: nvm, misread
There is a very easy way to do this.
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
Here's a classic mechanics question:




}{\sqrt{v^{4} + r^{2}g^{2}}} \textup {newtons.} )
Here's a classic mechanics question:
Paradoxica
-insert title here-
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
Ah I think I have the answer, let me write up a solution
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon

Finally a question from Paradoxica which I could actually do

Finally a question from Paradoxica which I could actually do
Paradoxica
-insert title here-
Re: HSC 2015 4U Marathon
that's correct, but not as quick. try thinking in the complex plane. also, in the question, I would not have stated the hypotenuse lengths were it not for the confusion.
Finally a question from Paradoxica which I could actually do
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
Ah yes I see it now. Both methods are quite efficient, in my opinionthat's correct, but not as quick. try thinking in the complex plane. also, in the question, I would not have stated the hypotenuse lengths were it not for the confusion.
asdfghjklqwerty
Member
- Joined
- Sep 14, 2015
- Messages
- 33
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
A 3 metre string AB has a mass of 5kg attached at point B. The string is rotated in a horizontal circle about A and breaks as soon as it exceeds a speed of rotation of 45 revolutions per minute.
i.Find the maximum possible tension in the string.
ii. the mass at B is replaced by a 3kg mass and an additional 1kg mass is attached to the string at C, 2 metres from A (as shown below). Find the new maximum number of revolutions per minute that the string can be rotated.
i need help with part ii now ( thanks
( thanks
ans: 52.5revs/minute
A 3 metre string AB has a mass of 5kg attached at point B. The string is rotated in a horizontal circle about A and breaks as soon as it exceeds a speed of rotation of 45 revolutions per minute.
i.Find the maximum possible tension in the string.
ii. the mass at B is replaced by a 3kg mass and an additional 1kg mass is attached to the string at C, 2 metres from A (as shown below). Find the new maximum number of revolutions per minute that the string can be rotated.
i need help with part ii now
ans: 52.5revs/minute
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon


)

 \frac{cos\theta}{r} )
 $ F= \frac{mg(V^2 -v^2)}{\sqrt{v^4 +r^2g^2}} )
Here's a classic mechanics question:
}{\sqrt{v^{4} + r^{2}g^{2}}} \textup {newtons.} )
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon

that's correct, but not as quick. try thinking in the complex plane. also, in the question, I would not have stated the hypotenuse lengths were it not for the confusion.

Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 2015 4U Marathon
Is i's answer 37 Newtons?A 3 metre string AB has a mass of 5kg attached at point B. The string is rotated in a horizontal circle about A and breaks as soon as it exceeds a speed of rotation of 45 revolutions per minute.
i.Find the maximum possible tension in the string.
ii. the mass at B is replaced by a 3kg mass and an additional 1kg mass is attached to the string at C, 2 metres from A (as shown below). Find the new maximum number of revolutions per minute that the string can be rotated.
i need help with part ii now( thanks
ans: 52.5revs/minute
asdfghjklqwerty
Member
- Joined
- Sep 14, 2015
- Messages
- 33
- Gender
- Male
- HSC
- 2015
Re: HSC 2015 4U Marathon
part i was what i just posted before. the answer for it is (135pi^2)/4=333.1 N
part i was what i just posted before. the answer for it is (135pi^2)/4=333.1 N
- Status
- Not open for further replies.
