I'm not sure if there's much mathematical merit behind this, but if p, q and r are positive integers, wouldn't the only case for which
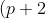(q+2)(r+2) = 64 )
holds true be when p = q = r = 2 (pqr = 8)?
p, q or r cannot equal 1, since 3 isn't a factor of 64.
When any of them are an integer greater than 2, there's no possible way to make 64 from the 3 sets of brackets. If p = 3, 4, 5, then p + 2 = 5, 6 or 7, which aren't factors of 64. If p = 6 (p + 2 = 8), then (q+2)(r+2) = 8, which can't be true, since each set of brackets must be greater than or equal to 3. Any number greater than 6 will have the same result.
The only other time
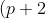(q+2)(r+2) = 64 )
holds true is if we include 0 as a positive integer (which isn't right). If p = 0, then (q+2)(r+2) = 32, which can be made with q = 2 and r = 6, for example. In this case, pqr = 0 < 8.
I hope that makes some sense.

