Complex Numbers - Help needed (1 Viewer)

[a1079atw]

Hi all,


Can anyone please help me with these three questions? I really have no idea how to solve them...

Thanks in advance!

 

[Sy123]

I'll give you some hints:

7) You can do the sub u=x^2 then solve the quadratic, or:



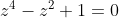
Multiply both sides by (z^2+1)



8)Similarly do a substitution or multiply both sides by (z^2-1)

9) We re-arrange:





Then roots of unity.

 

[QZP]

@Sy123, I'm not sure what you did for (z^2 +- 1). Care to explain?

 

[a1079atw]

Thanks I scanned my solution for Q7, but not sure if I did the right thing There are four answers?

I'm still working on Q9

 

[hit patel]

U did sillies a1079atw. Please check z^2= 1+....... and then u continued on with z = 1+....

I'll give you some hints:

7) You can do the sub u=x^2 then solve the quadratic, or:



Multiply both sides by (z^2+1)



8)Similarly do a substitution or multiply both sides by (z^2-1)

9) We re-arrange:





Then roots of unity.

Like this?

((z-1)/(z+1))^6=-1
(z-1)/(z+1)= [cis((2kpi+pi)/6)]


Now z-1= (z+1)(cis ((2pi+pi)/6))
z-1 = zcis ((2kpi+pi)/6))+ cis(cis ((2pi+pi)/6)
Since z is factorable

z(1- cis((2kpi+pi)/6)) -1 = cis ((2kpi+pi)/6)
Therefore z= (1+(cis ((2pi+pi)/6))) / (1- (cis ((2pi+pi)/6)))
Now we change to polar form:

z= (1+ cos ((2pi+pi)/6) + i sin ((2pi+pi)/6))/ (1- cos ((2pi+pi)/6) - i sin ((2pi+pi)/6))
Now using double angle

z= (2cos^2((2kpi+pi)/12) + 2icos ((2kpi+pi)/12) x sin ((2kpi+pi)/12)) / (2sin^2((2kpi+pi)/12) - 2i cos((2kpi+pi)/12) x sin((2kpi+pi)/12))

Factorising we get :
(2cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( 2sin ((2kpi+pi)/12) x (sin((2kpi+pi)/12) - i cos((2kpi+pi)/12)))

Now we can take out the -i from the denominator and set in it the polar form x + iy

This leads to :
(cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( -isin ((2kpi+pi)/12) x ( cos ((2kpi+pi)/12) + sin((2kpi+pi)/12))))

This leads to cot ((2kpi+pi)/12)/(-i )

= i cot((2kpi+pi)/12)
let k=0,+_ 1, +_2, -3

Now can find solutions.

 

[Drongoski]

Q7 & Q8 can also be done this way (for Q7):



Then you find z from there.


Sy123's method cleaner: you solve z^6 + 1 = 0. But don't forget to exclude roots for z^2 + 1 = 0.

 

[Sy123]

@Sy123, I'm not sure what you did for (z^2 +- 1). Care to explain?

I multiplied both sides of the equation by (z^2+1), this is because:



Which becomes easier to deal with.

NOTE: If you've done Series in 2U (if you haven't ignore), then notice that the sum 1 - z^2 + z^4 is a geometric series of ratio (-z^2) therefore we can use the sum formula so that this factorization becomes obvious.

Thanks I scanned my solution for Q7, but not sure if I did the right thing There are four answers?
View attachment 28762
I'm still working on Q9

The substitution method is very clunky, its better to just multiply both sides by (z^2+1)







BUT, we must discard the solutions that give us:



This is because those solutions only came about because we multiplied both sides by which creates more solutions.

U did sillies a1079atw. Please check z^2= 1+....... and then u continued on with z = 1+....




Like this?

((z-1)/(z+1))^6=-1
(z-1)/(z+1)= [cis((2kpi+pi)/6)]


Now z-1= (z+1)(cis ((2pi+pi)/6))
z-1 = zcis ((2kpi+pi)/6))+ cis(cis ((2pi+pi)/6)
Since z is factorable

z(1- cis((2kpi+pi)/6)) -1 = cis ((2kpi+pi)/6)
Therefore z= (1+(cis ((2pi+pi)/6))) / (1- (cis ((2pi+pi)/6)))
Now we change to polar form:

z= (1+ cos ((2pi+pi)/6) + i sin ((2pi+pi)/6))/ (1- cos ((2pi+pi)/6) - i sin ((2pi+pi)/6))
Now using double angle

z= (2cos^2((2kpi+pi)/12) + 2icos ((2kpi+pi)/12) x sin ((2kpi+pi)/12)) / (2sin^2((2kpi+pi)/12) - 2i cos((2kpi+pi)/12) x sin((2kpi+pi)/12))

Factorising we get :
(2cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( 2sin ((2kpi+pi)/12) x (sin((2kpi+pi)/12) - i cos((2kpi+pi)/12)))

Now we can take out the -i from the denominator and set in it the polar form x + iy

This leads to :
(cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( -isin ((2kpi+pi)/12) x ( cos ((2kpi+pi)/12) + sin((2kpi+pi)/12))))

This leads to cot ((2kpi+pi)/12)/(-i )

= i cot((2kpi+pi)/12)
let k=0,+_ 1, +_2, -3

Now can find solutions.

Yea something like that

 

[a1079atw]

U did sillies a1079atw. Please check z^2= 1+....... and then u continued on with z = 1+....

Thanks for the working of Q9, but I don't understand what's wrong with the z=1+...... part.
Don't you use this equation where z^n = a+bi is z^2= [cos(pi/3)+isin(pi/3)]?

 

[a1079atw]

@Drongoski
Thanks. Definitely clear things up!

 

[a1079atw]

@Sy123
Thank you, finally understand now

 

[hit patel]

Thanks for the working of Q9, but I don't understand what's wrong with the z=1+...... part.
Don't you use this equation where z^n = a+bi is z^2= [cos(pi/3)+isin(pi/3)]?
View attachment 28767

Np. Well its ok, i mislooked what you did.

 

[a1079atw]

Haha that's good