-
Coming soon...BoS Trial exams Watch this space!
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Complex Numbers - Help needed (1 Viewer)
- Thread starter a1079atw
- Start date
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
I'll give you some hints:
7) You can do the sub u=x^2 then solve the quadratic, or:
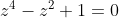
Multiply both sides by (z^2+1)
(z^4-z^2+1) = 0 )
8)Similarly do a substitution or multiply both sides by (z^2-1)
9) We re-arrange:
^6 = - (z+1)^6 )
^6 = -1 )
Then roots of unity.
7) You can do the sub u=x^2 then solve the quadratic, or:
Multiply both sides by (z^2+1)
8)Similarly do a substitution or multiply both sides by (z^2-1)
9) We re-arrange:
Then roots of unity.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
U did sillies a1079atw. Please check z^2= 1+....... and then u continued on with z = 1+....
((z-1)/(z+1))^6=-1
(z-1)/(z+1)= [cis((2kpi+pi)/6)]
Now z-1= (z+1)(cis ((2pi+pi)/6))
z-1 = zcis ((2kpi+pi)/6))+ cis(cis ((2pi+pi)/6)
Since z is factorable
z(1- cis((2kpi+pi)/6)) -1 = cis ((2kpi+pi)/6)
Therefore z= (1+(cis ((2pi+pi)/6))) / (1- (cis ((2pi+pi)/6)))
Now we change to polar form:
z= (1+ cos ((2pi+pi)/6) + i sin ((2pi+pi)/6))/ (1- cos ((2pi+pi)/6) - i sin ((2pi+pi)/6))
Now using double angle
z= (2cos^2((2kpi+pi)/12) + 2icos ((2kpi+pi)/12) x sin ((2kpi+pi)/12)) / (2sin^2((2kpi+pi)/12) - 2i cos((2kpi+pi)/12) x sin((2kpi+pi)/12))
Factorising we get :
(2cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( 2sin ((2kpi+pi)/12) x (sin((2kpi+pi)/12) - i cos((2kpi+pi)/12)))
Now we can take out the -i from the denominator and set in it the polar form x + iy
This leads to :
(cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( -isin ((2kpi+pi)/12) x ( cos ((2kpi+pi)/12) + sin((2kpi+pi)/12))))
This leads to cot ((2kpi+pi)/12)/(-i )
= i cot((2kpi+pi)/12)
let k=0,+_ 1, +_2, -3
Now can find solutions.
Like this?I'll give you some hints:
7) You can do the sub u=x^2 then solve the quadratic, or:
Multiply both sides by (z^2+1)
8)Similarly do a substitution or multiply both sides by (z^2-1)
9) We re-arrange:
Then roots of unity.
((z-1)/(z+1))^6=-1
(z-1)/(z+1)= [cis((2kpi+pi)/6)]
Now z-1= (z+1)(cis ((2pi+pi)/6))
z-1 = zcis ((2kpi+pi)/6))+ cis(cis ((2pi+pi)/6)
Since z is factorable
z(1- cis((2kpi+pi)/6)) -1 = cis ((2kpi+pi)/6)
Therefore z= (1+(cis ((2pi+pi)/6))) / (1- (cis ((2pi+pi)/6)))
Now we change to polar form:
z= (1+ cos ((2pi+pi)/6) + i sin ((2pi+pi)/6))/ (1- cos ((2pi+pi)/6) - i sin ((2pi+pi)/6))
Now using double angle
z= (2cos^2((2kpi+pi)/12) + 2icos ((2kpi+pi)/12) x sin ((2kpi+pi)/12)) / (2sin^2((2kpi+pi)/12) - 2i cos((2kpi+pi)/12) x sin((2kpi+pi)/12))
Factorising we get :
(2cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( 2sin ((2kpi+pi)/12) x (sin((2kpi+pi)/12) - i cos((2kpi+pi)/12)))
Now we can take out the -i from the denominator and set in it the polar form x + iy
This leads to :
(cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( -isin ((2kpi+pi)/12) x ( cos ((2kpi+pi)/12) + sin((2kpi+pi)/12))))
This leads to cot ((2kpi+pi)/12)/(-i )
= i cot((2kpi+pi)/12)
let k=0,+_ 1, +_2, -3
Now can find solutions.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
I multiplied both sides of the equation by (z^2+1), this is because:@Sy123, I'm not sure what you did for (z^2 +- 1). Care to explain?
Which becomes easier to deal with.
NOTE: If you've done Series in 2U (if you haven't ignore), then notice that the sum 1 - z^2 + z^4 is a geometric series of ratio (-z^2) therefore we can use the sum formula so that this factorization becomes obvious.
The substitution method is very clunky, its better to just multiply both sides by (z^2+1)ThanksI scanned my solution for Q7, but not sure if I did the right thing
There are four answers?
View attachment 28762
I'm still working on Q9
BUT, we must discard the solutions that give us:
This is because those solutions only came about because we multiplied both sides by
Yea something like thatU did sillies a1079atw. Please check z^2= 1+....... and then u continued on with z = 1+....
Like this?
((z-1)/(z+1))^6=-1
(z-1)/(z+1)= [cis((2kpi+pi)/6)]
Now z-1= (z+1)(cis ((2pi+pi)/6))
z-1 = zcis ((2kpi+pi)/6))+ cis(cis ((2pi+pi)/6)
Since z is factorable
z(1- cis((2kpi+pi)/6)) -1 = cis ((2kpi+pi)/6)
Therefore z= (1+(cis ((2pi+pi)/6))) / (1- (cis ((2pi+pi)/6)))
Now we change to polar form:
z= (1+ cos ((2pi+pi)/6) + i sin ((2pi+pi)/6))/ (1- cos ((2pi+pi)/6) - i sin ((2pi+pi)/6))
Now using double angle
z= (2cos^2((2kpi+pi)/12) + 2icos ((2kpi+pi)/12) x sin ((2kpi+pi)/12)) / (2sin^2((2kpi+pi)/12) - 2i cos((2kpi+pi)/12) x sin((2kpi+pi)/12))
Factorising we get :
(2cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( 2sin ((2kpi+pi)/12) x (sin((2kpi+pi)/12) - i cos((2kpi+pi)/12)))
Now we can take out the -i from the denominator and set in it the polar form x + iy
This leads to :
(cos((2kpi+pi)/12) x (cos((2kpi+pi)/12)+ sin((2kpi+pi)/12))/ ( -isin ((2kpi+pi)/12) x ( cos ((2kpi+pi)/12) + sin((2kpi+pi)/12))))
This leads to cot ((2kpi+pi)/12)/(-i )
= i cot((2kpi+pi)/12)
let k=0,+_ 1, +_2, -3
Now can find solutions.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Np.Thanks for the working of Q9, but I don't understand what's wrong with the z=1+...... part.
Don't you use this equation where z^n = a+bi is z^2= [cos(pi/3)+isin(pi/3)]?
View attachment 28767