Last edited:
-
Interested in being a marker for this year's BoS Maths Trials? Let us know before 31 August, see this thread for details
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012 MX2 Marathon (archive) (1 Viewer)
- Thread starter nightweaver066
- Start date
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
gurmies
Drover
Re: 2012 HSC MX2 Marathon
Possibly a simpler way to do this would be to use the sum of roots to find the final root, and the product of roots to find d.
Re: 2012 HSC MX2 Marathon
 $ and $ Q(a\cos\phi,b\sin\phi) $ lie on the ellipse $ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. \\\\ $Find the equation of line $PQ)
I used sum of roots to find the final root, then subbed in x=-1/2 to find d. But either way works.Possibly a simpler way to do this would be to use the sum of roots to find the final root, and the product of roots to find d.
Last edited:
gurmies
Drover
Re: 2012 HSC MX2 Marathon
I suspect that it's sufficient to solve Z=Z^3 and discard -1 as a solution. My reasoning is that there clearly can't be an imaginary part present in Z. With this in mind, we can proceed noting that |Z| = Z, Z > 0 and |Z| = -Z, Z < 0. My method yields Z = 0 or/ 1. Could be wrong here though.
Last edited:
Re: 2012 HSC MX2 Marathon
I asked that question in 2009, and you answered it oO.Prove that:
if and only if

Re: 2012 HSC MX2 Marathon
From memory, I think there's an easier way to do this question. Ie. using z z (bar) = |z|^2
gurmies
Drover
Re: 2012 HSC MX2 Marathon
\overline{(z-2)}=3 \\\\ (z-2)(\overline{z}-2)=3 \\\\ z\overline{z}-2z-2\overline{z}+4=3 \\\\ z\overline{z}-2z-2\overline{z}+1=0 \\\\ 2z\overline{z}-4z-4\overline{z}+2=0 \\\\ 3z\overline{z}-3z-3\overline{z}+3=z\overline{z}+z+\overline{z}+1 \\\\ 3(z\overline{z}-z-\overline{z}+1)=z\overline{z}+z+\overline{z}+1 \\\\ 3(z-1)(\overline{z}-1)=(z+1)(\overline{z}+1) \\\\ 3(z-1)\overline{(z-1)}=(z+1)\overline{(z+1)} \\\\ 3|z-1|^{2}=|z+1|^{2})
largarithmic
Member
- Joined
- Aug 9, 2011
- Messages
- 195
- Gender
- Male
- HSC
- 2011
Re: 2012 HSC MX2 Marathon
http://en.wikipedia.org/wiki/Circles_of_Apollonius
It's also true because ofFrom memory, I think there's an easier way to do this question. Ie. using z z (bar) = |z|^2
http://en.wikipedia.org/wiki/Circles_of_Apollonius
Nooblet94
Premium Member
- Joined
- Feb 5, 2011
- Messages
- 1,041
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
Haven't seen many graphing questions, so here we go.
Graph the following parametric equation:
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" title="\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" /></a>

Haven't seen many graphing questions, so here we go.
Graph the following parametric equation:
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" title="\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" /></a>
rolpsy
Member
- Joined
- Apr 9, 2011
- Messages
- 94
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
lol

question:
graph
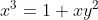
(perhaps a tad more accessible than that ^)
lol
question:
graph
(perhaps a tad more accessible than that ^)
Attachments
-
38.1 KB Views: 194
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: 2012 HSC MX2 Marathon
Rolpsy, what program was used to sketch that curve?
Rolpsy, what program was used to sketch that curve?
rolpsy
Member
- Joined
- Apr 9, 2011
- Messages
- 94
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
texshop (i.e. latex) with pstricks (and pst-plot)Rolpsy, what program was used to sketch that curve?
Re: 2012 HSC MX2 Marathon
nooblet what are you trying to imply here?Haven't seen many graphing questions, so here we go.
Graph the following parametric equation:
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" title="\\ x=16\sin^3(t)\\ y=13\cos(t)-5\cos(2t)-2\cos(3t)-\cos(4t)" /></a>

deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
I haven't seen many integration questions... This is from someone at school (you know who you are )
)
<a href="http://www.codecogs.com/eqnedit.php?latex=\int sin(lnx)dx" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\int sin(lnx)dx" title="\int sin(lnx)dx" /></a>
I haven't seen many integration questions... This is from someone at school (you know who you are
<a href="http://www.codecogs.com/eqnedit.php?latex=\int sin(lnx)dx" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\int sin(lnx)dx" title="\int sin(lnx)dx" /></a>
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: 2012 HSC MX2 Marathon
dx)

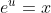

 dx = \int e^usinudu)

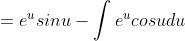
)
)

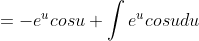
)
 + (2): 2\int e^u sinu du = 2e^u(sinu - cosu) - 2\int e^u sinu du )
)
)
 + c)


