ProdigyInspired
Tafe Advocate
- Joined
- Oct 25, 2014
- Messages
- 643
- Gender
- Male
- HSC
- 2016
The question is:
Using the parallelogram method along with a diagram, why:
a. |z1 + z2| <= |z1| + |z2|
What conditions need to occur for |z1 + z2| = |z1| + |z2|?
Similarly
b. |z1 - z2| <= |z1| - |z2|
What conditions need to occur for |z1 - z2| = |z1| - |z2|?
[HR][/HR]
I've given a try for a.
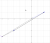
Drew a parallelogram, with z1 and z2 as the sides. From the point where the vectors originate, I drew a diagonal, naming it z1+z2.
Now with triangle properties, it is known that one side cannot be larger than the sum of the other two.
Therefore, a triangle with the sides z1 and z2, and the length side (z1 + z2), would have |z1 + z2| being less than |z1| + |z2|.
For LHS = RHS, all the vectors have to be the same length, therefore z1 must be = z2.
Using the parallelogram method along with a diagram, why:
a. |z1 + z2| <= |z1| + |z2|
What conditions need to occur for |z1 + z2| = |z1| + |z2|?
Similarly
b. |z1 - z2| <= |z1| - |z2|
What conditions need to occur for |z1 - z2| = |z1| - |z2|?
[HR][/HR]
I've given a try for a.
Drew a parallelogram, with z1 and z2 as the sides. From the point where the vectors originate, I drew a diagonal, naming it z1+z2.
Now with triangle properties, it is known that one side cannot be larger than the sum of the other two.
Therefore, a triangle with the sides z1 and z2, and the length side (z1 + z2), would have |z1 + z2| being less than |z1| + |z2|.
For LHS = RHS, all the vectors have to be the same length, therefore z1 must be = z2.
Last edited: