hscishard
Active Member
x^2 -1
You're askingh for the general one, arent you?
You're askingh for the general one, arent you?
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
yesx^2 -1
You're askingh for the general one, arent you?
What terms should be in there?
i know it's easy for u guys...
but i still don't know how to solve it by multiplying the square of the denominator.
greatly appreciated if someone can help
mmm hsc 2012, looking to get a head start?
First step: exclude values where denominator=0 { however, you will see this only matters when you have a "less than or equal" or a "greater than or equal"}
(2x+5)(x+1)^2 / (x+1) < 3(x+1)^2 { DONT EXPAND, it is easier to move all terms to one side and factorise, saves time}
(2x+5)(x+1)-3(x+1)^2 <0
(x+1) { (2x+5) -3(x+1) } <0
(x+1)( 2-x) <0
x<-1, x > 2 ( if you need explaination from the previous step to this one please ask)
thank you so much
shat brix
For some reason, I don't think that's correct
New Question:
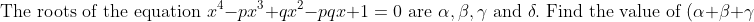(\alpha+\beta+\delta)(\beta+\gamma+\delta)(\alpha+\gamma+\delta))
The trick is to find a shortcut, it can be done in a few lines.thats not hard, just long, get some interesting questions lol
The trick is to find a shortcut, it can be done in a few lines.
lol what expand ( p -a) ( p-b) (p-c) ( p-d), where a, b, c, d are roots
its a little less work i guess
I felt special because I was the only one in class who thought of that.
