Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Please help with this question (1 Viewer)
- Thread starter kimtuluu
- Start date
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,101
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Sub 2pi into the equation?
That's what I did but then stuck as the question asks for distance not displacementSub 2pi into the equation?
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,101
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Just say to the right.
The above equation is displacement so unfortunately won't answer "how far" the particle travels (distance) if we were to just sub in 2pi. I think possibly finding the distance travelled between 0 and pi/2 on the sin curve (since it's all in one direction) then multiply by 4 (to complete the 4 quadrants of the sin curve) should give you how far it travelled in total.
Sorry for giving a really bad wording of the explanation (there should be a more formal way of explaining but I am a lil rusty)
Sorry for giving a really bad wording of the explanation (there should be a more formal way of explaining but I am a lil rusty)
Last edited:
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,101
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
ExtremelyBoredUser
Bored Uni Student
Hey, so this is pretty much what I did to find the distance.
I use the double angle identity; cos2x= 1 - 2sin^2x and rearranged it, I got 2sin^2x = 1-cos2x
Substituting:
x = 2+ 2(1-cos2t)
= 2 + 2 - 2cos2t
= 4 - 2cos2t
This is in a way better form because now you can find the period.
T = 2pi/n = 2pi/2 = pi
So now you know that one whole period is pi seconds, you should find the distance from 0 to pi/4 to get a scalar quantity.
x = 4 - 2cos(2*pi/4) = 4
Now since we know that the distance from 0 to pi4 is 4, we just need to multiply it by the amount of times to get to 2pi.
There's 8 strands of the 0-pi/4 distance in 2pi. pi/4*8 = 2pi.
Hence 8* 4= 32m
This is an algebraic way of doing it and what I did to save time but an alternative method (and much more safer) is simply graphing the function when you find it in the 4 - 2cos2x stage if you feel comfortable with doing that. I'm sure there's better ways of doing this but this is what came to my mind when first seeing the question.
I use the double angle identity; cos2x= 1 - 2sin^2x and rearranged it, I got 2sin^2x = 1-cos2x
Substituting:
x = 2+ 2(1-cos2t)
= 2 + 2 - 2cos2t
= 4 - 2cos2t
This is in a way better form because now you can find the period.
T = 2pi/n = 2pi/2 = pi
So now you know that one whole period is pi seconds, you should find the distance from 0 to pi/4 to get a scalar quantity.
x = 4 - 2cos(2*pi/4) = 4
Now since we know that the distance from 0 to pi4 is 4, we just need to multiply it by the amount of times to get to 2pi.
There's 8 strands of the 0-pi/4 distance in 2pi. pi/4*8 = 2pi.
Hence 8* 4= 32m
This is an algebraic way of doing it and what I did to save time but an alternative method (and much more safer) is simply graphing the function when you find it in the 4 - 2cos2x stage if you feel comfortable with doing that. I'm sure there's better ways of doing this but this is what came to my mind when first seeing the question.
Last edited:
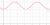
To find distance travelled, you need the starting and finishing positions - that is,  at
at 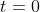 and at
and at 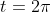 - and its position whenever it stops moving - that is, when
- and its position whenever it stops moving - that is, when 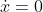 - in case it changes direction.
- in case it changes direction.
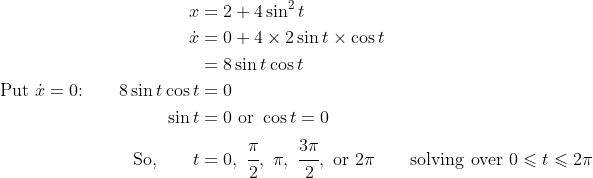
^2 = 2\ \text{m})
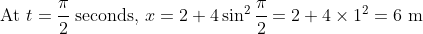
^2 = 2\ \text{m})
^2 = 6\ \text{m})
^2 = 2\ \text{m})
So, the distance travelled in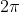 seconds is
seconds is 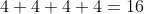 metres.
metres.
So, the distance travelled in
There is an error here... atx = 4 - 2cos2t
This is in a way better form because now you can find the period.
T = 2pi/n = 2pi/2 = pi
So now you know that one whole period is pi seconds, you should find the distance from 0 to pi/4 to get a scalar quantity.
x = 4 - 2cos(2*pi/4) = 4
Now since we know that the distance from 0 to pi4 is 4, we just need to multiply it by the amount of times to get to 2pi.
There's 8 strands of the 0-pi/4 distance in 2pi. pi/4*8 = 2pi.
Hence 8* 4= 32m
Note also that this method only works so long as the times chosen do not include any change in the direction of motion. This is not a problem for the time period selected here, however.
ExtremelyBoredUser
Bored Uni Student
There is an error here... at,
, and so the distance travelled in a quarter of a period is 2 m, from
to
, making the total distance
metres. The above answer has mistakenly taken the quarter-period distance as 4 m, which is why its answer of 32 m disagrees with my answer of 16 m.
Note also that this method only works so long as the times chosen do not include any change in the direction of motion. This is not a problem for the time period selected here, however.
Ahhh. The wave starts at x=2 and from t=0 to t=2 the distance is x=2 to x=6 so I should've done (4-2)*8. My bad. I should've checked t = 0 to find the displacement it starts, or simply c in the original function, and then the displacement at t = pi/4.

Last edited:
Thank you very much. This is a perfect working out I am looking for.To find distance travelled, you need the starting and finishing positions - that is,at
and at
- and its position whenever it stops moving - that is, when
- in case it changes direction.
So, the distance travelled inseconds is
metres.