-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Please Factorise (1 Viewer)
- Thread starter Drongoski
- Start date
For Q1 or Q2?my final answer isbut i did it really fast so
i might of made an error. All I did was factorise using sum and difference of 2 cubes
Shadowdude
Cult of Personality
- Joined
- Sep 19, 2009
- Messages
- 12,141
- Gender
- Male
- HSC
- 2010
WolframAlpha is your friend.
The first one apparently gives:(a^{2}-c^{2})(b^{2}-c^{2}))
Second is apparently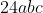
The first one apparently gives:
Second is apparently
kaz1
et tu
was bored, couldn't do no.1
no. 2 is 24abc
no. 2 is 24abc
Not bad. How about Q1? Wolfram is a Genius. Shadow has given the right answers. But how do you do them?yeh it is 24abc i forgot the extra 4
Good effort anyway.was bored, couldn't do no.1
no. 2 is 24abc
You don't have to expand it, jus factorise immediatelyfor Q2, expand it out, then + and - a^2*b^2*c^2. From there, rearrange and factorize. It really helps working it out.
Manipulation techniques really come in handy.
As difference and sum of cubes instead
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
No one wanted to do Q1. 
 + b^4(c^2-a^2) + c^4(a^2-b^2))
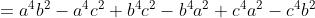
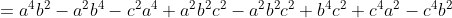
(a^2-c^2))
-c^2(a^2-b^2)](a^2-c^2))
(a^2-c^2)(a^2-b^2))
(b+c)(a-c)(a+c)(a-b)(a+b))
Last edited:
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
This thread made me want to learn cyclic expansion & factorisation. Still new, it's hard to find information about it online..
Unsure if the way i set out the solution is correct or not..
 Let $ f(a, b, c) = (a + b + c)^3 - (b + c - a)^3 - (c + a - b)^3 - (a + b - c)^3)
 = (a + b + c)^3 - (a + c - b)^3 - (c + b - a)^3 - (a + b - c)^3)
)

 = (b + c)^3 - (b + c)^3 - (c - b)^3 - (b - c)^3)
^3 + (c - b)^3)
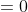

] = 3)
^3 - (a + c - b)^3 - (c + b -a)^3 - (a + b - c)^3 $ where K is a real number)

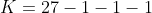
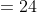
 = 24abc)
Unsure if the way i set out the solution is correct or not..
4025808
Well-Known Member
oh woops my bad I meant Q1You don't have to expand it, jus factorise immediately
As difference and sum of cubes instead
- Joined
- Feb 16, 2005
- Messages
- 8,564
- Gender
- Male
- HSC
- 2006
- Joined
- Feb 16, 2005
- Messages
- 8,564
- Gender
- Male
- HSC
- 2006
I think you have to show it is equal for all variations to prove it is a cyclic expressionThis thread made me want to learn cyclic expansion & factorisation. Still new, it's hard to find information about it online..
Unsure if the way i set out the solution is correct or not..
 = 24abc)
i.e. prove f(a, b, c) = f(a, c, b) = f(b, a, c) = f(b, c, a) = f(c, a, b) = f(c, b, a)
gurmies
Drover
Typically you do, but the above is clearly cyclic.I think you have to show it is equal for all variations to prove it is a cyclic expression
i.e. prove f(a, b, c) = f(a, c, b) = f(b, a, c) = f(b, c, a) = f(c, a, b) = f(c, b, a)

