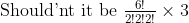Perms and Combs (1 Viewer)

[HeroWise]

How many ways can you arrange COMBINATION so that the vowels are in alphabetical order and separated from each other by at least 1 consonant






6! ways to arrange the consonants

Repetitions:

2! of N
2! of I
2! of O

and thre are 3 different cases where the vowels are separated by only one

 

[Roy G Biv]

Explanation:
6 consonants - 6! / 2!
Self explanatory

Vowels have to be separated by at least 1 consonant. (BTW, seems as if you're mistaking "separated by 1 vowel" with "separated by AT LEAST 1 vowel". at least means separation by 2 [or more] is fine too. So it's possible to have: VCVCCVCVCCV)

Method I'm going to use:
I'm going to fit in the vowels "in between the consonants". I've arranged the consonants above, but I've left a gap between each consonant, as well as 1 gap before and 1 gap after. After attaining 6!/2!, I now have to fit in 5 vowels into 7 spaces that have been created.

However, there is an ugly restriction: the vowels also have to be in alphabetical order.

Honestly, I couldn't figure out a short cut way, I just brute forced it.
Umbrella case 1: C C a C blank C blank C blank C blank <-- have to fit in 2o's and 2 i's into the 4 blanks. only 1 way to do this, since i's have to be before o's, and they're interchangeable.

Umbrella case 2: C a C blank C

ah cbf, just check my working out. If you don't understand, let me know and I'll elaborate more, but it should be self-explanatory. I just brute-forced it really.

I'm getting:
6!/2! x (1 + 5 + 15)
= 6!/2! x (21)

Probably made a silly mistake somewhere heh, but hope you see how I did it.

PS: how can I insert an image such that it appears as an image rather than a link?

edit million'th because not satisfied with ugly, brute-force method:
Alternative solution-
6!/2! x (7P5/2!2! / [5!/2!2!]) = 7560

6!/2! for consonants = 360
7P5/2!2! = ways to arrange vowels in between the consonants
then divide further by the number of ways to arrange the vowels amongst themselves, as only 1 of those will have them all in alphabetical order.

now THAT is fkn neat. IF it's correct. and I'm pretty sure it is. i think. i hope.

 

[Roy G Biv]

Can I please know where that question is from?

 

[HeroWise]

Im doing random questions i found on the internet, if im not wrong its a 'boderline' 3u question.

I have realised its in the 4u perms and combs thread but i originally got it from a friend who is compiling these questions


http://community.boredofstudies.org...rmutations-combinations-marathon-archive.html



I am going to see your post in a bit and ill see if i need help ill ask you again ahahah,

Thanks anyway

 

[Roy G Biv]

Ah, at least I know I got the question right

I'm 99.93% sure you won't face a question of this level in a 3u exam. I base that on the fact that, after searching ~1515 OCR'd 3u trials, I've come across only 1 other question similar to this- james ruse 3u 2003 trial, q7.

tbh, i wouldn't use that thread to prepare for hsc perms/combs. just use past paper questions. not international mathematical olympiad questions :| and god knows where else those questions are sourced from.

 

[HeroWise]

AHAHAH
anyway its a good way to grasp perms and combs, the trial questions, majority of them just repeat themselves.

 

[HeroWise]

Holy crap.... its litereally the same question LOL

 

[Roy G Biv]

lol yeah, basically the same thing.

if you want a good revision, check out the old coroneos (and I mean like, the REALLY old coroneos one, the one for the previous syllabus) revision set. someone has scanned the book, google up "coroneos filetypedf" and it'll be a few entries down.

or check 4u textbooks (eg terry lee 4u) or 4u past papers.

I daresay it'll be more relevant and useful than stuff which is not in the syllabus, such as some of the questions in that thread. just my humble opinion anyway.