It's essentially just saying that
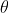
is uniformly distributed, resulting in in a uniform distribution of lengths.
Consider this example: Suppose you wanted to plot an equal number of points around a unit circle. If you calculated the (x,y) coordinates from equal increments of theta, you'll end up with a uniform distribution of points. Now, try doing it by generating the y coordinates from equal increments of x coordinates. You'll find that the points aren't uniformly distributed - if you were to imagine plotting a huge number of points around the circle, most of the points will be skewed away from the left and right ends, because a small change in x there will lead to a large change in y (since the circle is very steep at x = +-1). In this case, the points are not uniformly distributed because the probability of picking a point with a small y value (near zero) will be much smaller than picking a point with a large y value (near 1) since most of the points have y-values skewed towards 1.
In our case, parameterisation by theta is correct since theta results in a uniform distribution. If you try to parameterise by h, you're more likely to get a longer chord length than a shorter chord length due to the steepness of the circle when h is small (this is analogous to the example above if you try to parameterise using x). When h is small, small changes to h result in small changes in L. When h is large, small changes in h result in large changes in L. Thus, the chord lengths are more skewed towards the larger values since there's a lot more closely spaced L values when h is small. This is also evident from the calculation: parameterisation by theta results in a value of 4/pi = 1.27, whereas parameterisation by h results in a value of pi/2 = 1.57. The value is significantly larger due to this skewed distribution.
\,d\theta)