-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Maximum value of f(x) given graph of f'(x) (1 Viewer)
- Thread starter SkyAngel
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
If f'(x) is positive, then f(x) is increasing
If f'(x) is negative, then f(x) is decreasing.
We note that f'(x) is positive for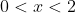 , then negative for all
, then negative for all 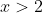
This means f(x) increases until x=2, and then decreases. Note that f'(2)=0 which means at x=2, f(x) does have a stationary point.
-------------------------
So we know that the maximum value is at x=2 using the above info. But then what is the value itself.
-------------------------
If this doesn't make sense, be worried:
The area under the curve y=f'(x) between a and b is
 dx } \\ =f\left( b \right) -f\left( a \right) )
So the area under the curve y=f'(x) between x=0 and x=2 is
 dx } \\ =f\left( 2 \right) -f\left( 0 \right) )
----------------------
Now, if the y-coordinate at x=2 is f(2)
And the y-coordinate at x=0 is f(0)
Then the DIFFERENCE between the y-coordinates is also f(2)-f(0)
This means, that the area under the curve in the derivative, is the change in y-value of the original function.
-----------------------------
This means, that if f(0) = 0 like the question said, and the area under the derivative between 0 and 2 is A1 = 4, then f(x) increases by 4 units from x=0 to x=2. So the maximum value is 4
If f'(x) is negative, then f(x) is decreasing.
We note that f'(x) is positive for
This means f(x) increases until x=2, and then decreases. Note that f'(2)=0 which means at x=2, f(x) does have a stationary point.
-------------------------
So we know that the maximum value is at x=2 using the above info. But then what is the value itself.
-------------------------
If this doesn't make sense, be worried:
The area under the curve y=f'(x) between a and b is
So the area under the curve y=f'(x) between x=0 and x=2 is
----------------------
Now, if the y-coordinate at x=2 is f(2)
And the y-coordinate at x=0 is f(0)
Then the DIFFERENCE between the y-coordinates is also f(2)-f(0)
This means, that the area under the curve in the derivative, is the change in y-value of the original function.
-----------------------------
This means, that if f(0) = 0 like the question said, and the area under the derivative between 0 and 2 is A1 = 4, then f(x) increases by 4 units from x=0 to x=2. So the maximum value is 4
Last edited:
Thank you so much! It all makes so much sense. I'm so sorry to bother you again but I can't figure out (iii) either.If f'(x) is positive, then f(x) is increasing
If f'(x) is negative, then f(x) is decreasing.
We note that f'(x) is positive for, then negative for all
This means f(x) increases until x=2, and then decreases. Note that f'(2)=0 which means at x=2, f(x) does have a stationary point.
-------------------------
So we know that the maximum value is at x=2 using the above info. But then what is the value itself.
-------------------------
If this doesn't make sense, be worried:
The area under the curve y=f'(x) between a and b is
So the area under the curve y=f'(x) between x=0 and x=2 is
----------------------
Now, if the y-coordinate at x=2 is f(2)
And the y-coordinate at x=0 is f(0)
Then the DIFFERENCE between the y-coordinates is also f(2)-f(0)
This means, that the area under the curve in the derivative, is the change in y-value of the original function.
-----------------------------
This means, that if f(0) = 0 like the question said, and the area under the derivative between 0 and 2 is A1 = 4, then f(x) increases by 4 units from x=0 to x=2. So the maximum value is 4
'Find the value of f(6)'. Please help me.
Thank you so much! It all makes so much sense. I'm so sorry to bother you again but I can't figure out (iii) either.
'Find the value of f(6)'. Please help me.
Last edited:
thank you! :d

