I don't know if this was the reason why, but in the Q you typed above, there's a typo (top-right entry should have 6 rather than 5 in the square root).I feel bad lol. I had the same idea as InteGrand, I just mucked up my matlab input when I went to check my answer
-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
MATH2601 Higher Linear Algebra (1 Viewer)
- Thread starter leehuan
- Start date
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Oops. Nah I think that was just a typo as I typed it on the forumsI don't know if this was the reason why, but in the Q you typed above, there's a typo (top-right entry should have 6 rather than 5 in the square root).
This one's a bit long...
Proven in i): 0 is the only eigenvalue of B (so B is nilpotent)
 Prove that for }k=1,\dots,m-1\\ B^k \textbf{v} \in \ker(B^{m-k})\backslash \ker(B^{m-k-1}))
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Oh of course. Once I drew out the Jordan chain again and looked carefully at what the question gave iii made sense.
_________________________________________
Tools permitted if useful: Binomial theorem for matrices that commute in multiplication, Cayley-Hamilton theorem
Edit: Thanks IG I just saw where your reply was
Last edited:
Hint: Use the axioms to show that a + a0 = a.No more questions for this sem after tomorrow.
__________________
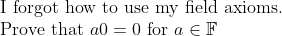
Well you wrote one up here before, so maybe you'd find that easiest to "memorise" for yourself:This is a highly open-ended question and everyone's opinion might be different.
What's the easiest proof (or would be a very easy proof) of the Cauchy-Schwarz inequality to memorise?
Note that it needs to be adapted slightly to deal with the complex case, but it's not too big a deal.
I did not even know that there was a sum form until doing past papers for 1251. Then I had to figure out why the sum and vector forms were equivalent.
You can also probably find many proofs online. There are twelve proofs here, but they seem to only be for the case of R^n: http://www.uni-miskolc.hu/~matsefi/Octogon/volumes/volume1/article1_19.pdf .
Last edited:
Yes. (I assume you meant the field to be R.)This is just some personal fun
\\ \text{where }x\oplus y = x\times y\\ x\otimes y = y^x\\ \text{Does there exist an inner product we can define to make it an inner product space?})
Last edited:
turtlesnore
New Member
- Joined
- Sep 21, 2015
- Messages
- 4
- Gender
- Male
- HSC
- 2015
Hopefully you don't mind if i post a question here. (taking MATH2601 this semester)
Suppose that G is a group with precisely three distinct elements e (the identity), a and b.
a) Prove that ab = e (Hint: eliminate other possibilities).
b) Prove that a^2 = b.
c) Deduce that G = {e, a, a^2} and hence that G is isomorphic to the group.
(How do you get LaTeX to work here?)
Suppose that G is a group with precisely three distinct elements e (the identity), a and b.
a) Prove that ab = e (Hint: eliminate other possibilities).
b) Prove that a^2 = b.
c) Deduce that G = {e, a, a^2} and hence that G is isomorphic to the group.
(How do you get LaTeX to work here?)
What was your progress on the questions so far?Hopefully you don't mind if i post a question here. (taking MATH2601 this semester)
Suppose that G is a group with precisely three distinct elements e (the identity), a and b.
a) Prove that ab = e (Hint: eliminate other possibilities).
b) Prove that a^2 = b.
c) Deduce that G = {e, a, a^2} and hence that G is isomorphic to the group.
(How do you get LaTeX to work here?)
Also to use LaTeX on the forums here, you need to enclose TeX code in so-called "tex tags". (Using LaTeX here is a bit different to just using it on your own computer.) You need to enclose the TeX code in between: [tex.] [/tex.] (but leave out the red dots).
For example: typing
[tex.] y = x^{2}[/tex.]
(but deleting the red dots) gives
turtlesnore
New Member
- Joined
- Sep 21, 2015
- Messages
- 4
- Gender
- Male
- HSC
- 2015
I thought about using the identity and inverse axioms but I couldn't get anywhere with them. I thought that it would be straight forward that  since there are only 3 elements in G, so either
since there are only 3 elements in G, so either  or
or  . But I was confused when I saw that part b said
. But I was confused when I saw that part b said  because that wouldn't be consistent with my result, and implies that
because that wouldn't be consistent with my result, and implies that  doesn't necessarily have to be written in G to be in the set G.
doesn't necessarily have to be written in G to be in the set G.
Thanks for the LaTeX help.
Thanks for the LaTeX help.
I thought about using the identity and inverse axioms but I couldn't get anywhere with them. I thought that it would be straight forward thatsince there are only 3 elements in G, so either
or
. But I was confused when I saw that part b said
because that wouldn't be consistent with my result, and implies that
doesn't necessarily have to be written in G to be in the set G.
Thanks for the LaTeX help.
turtlesnore
New Member
- Joined
- Sep 21, 2015
- Messages
- 4
- Gender
- Male
- HSC
- 2015
Thanks a bunch InteGrand!
