Is there a speicific rule for this? And where did you learn such things?
There are a couple of "rules". Firstly what khorne did was prime factorise the number, prime factorization is where you make a number completely out of primes, because every number can be expressed as the product of primes. To do so, you divide a number by a small prime and then continue this process until you end up at a prime number.
For example, take 72. The last digit is a multiple of 2, so we can easily tell that 2 is a factor. Dividing by 2 we get 36. So 72 = 2 x 36. But 36 is not a prime, so we observe that 36 is also divisible by 2. Dividing by 2 we get 18. So 36 = 2 x 18, and so 72 = 2 x (2 x 18) = 2 x 2 x 18. Continuing in this way we find 72 = 2 x 2 x 2 x 3 x 3
This can be written as 72 = 2
3 x 3
2.
Why do we prime factorize? We do this because it reveals alot of information about that number.
Another rule is to understand that for a number to be a perfect square, the prime factorization MUST have each numbers exponent as a multiple of 2. For example, lets look at the number 72 again, recall its prime factorization is 2
3 x 3
2
Take the square root of 72

remember:

so,


Now,
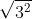
can easily be found, it is 3, because:
^{\frac{1}{2}} = 3^{\frac{1}{2} \times 2} = 3^1)
but
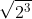
cannot be easily found, because as you know, it equals
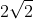
. So the square root of 72 is
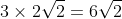
. But this number is not an integer, and so 72 is not a perfect square (as the root of a square must be an integer).
But if it were
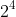
then the square root would be
^2} = 2^2)
So just note that a perfect squares prime factorization will have all its exponents (powers) as a multiple of 2.
The prime factorization of 2008 is 2
3 x 251.
So to make this a perfect square, we must multiply the 2
3 by 2 to get the power to be 4 (which is a multiple of 2), and to get 251 to be a multiple of 2 we must multiple 251 by 251 to get 251
2.
The new number is 2
4 x 251
2, and so as all its powers are a multiple of 2, then the number is a perfect square.
But the numbers we have to multiple 2008 by to get this perfect square by was 2 x 251, which is 502. This is indeed the answer.