leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,768
- Gender
- Male
- HSC
- 2015
Can someone check my working? I lost motivation to do it (because I'm timing myself doing a past paper) and now I can't force the final answer out, but just incase anything happened I want to know if what I had done was correct.

Need checked: Proof of parallel
Need help: Proving the length part.





\\ \Leftrightarrow = \left(1-\alpha\right) \textbf{a})
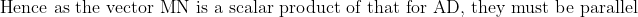
Wow that LaTeX took forever to type only to look so ugly
Need checked: Proof of parallel
Need help: Proving the length part.
Wow that LaTeX took forever to type only to look so ugly
