I've tried rearranging it and using various trig identities, but I kept going around in circles and not getting it into any recognisable form. Wolfram Alpha didn't help either
Integrating Logarithmic Functions (1 Viewer)
- Thread starter twinklegal19
- Start date
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Following the question, divide numerator and denominator by cos^2x, so
I've tried rearranging it and using various trig identities, but I kept going around in circles and not getting it into any recognisable form. Wolfram Alpha didn't help either
Now using a suitable substitution.. then partial fractions..
But I only know 2U methods lol. Don't think substituting/partial fractions is neededFollowing the question, divide numerator and denominator by cos^2x, so
Now using a suitable substitution.. then partial fractions..
Last edited:
Also not sure if it's a hard 2U question or easy 3U...
RealiseNothing
what is that?It is Cowpea
I don't think it's a 2U question, I can't think of how you would get 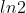 in the answer given those limits.
in the answer given those limits.
RealiseNothing
what is that?It is Cowpea
Unless it ends up being something like:
])
Then by subbing in the limits you would get that answer.
Then by subbing in the limits you would get that answer.
I don't think it's a 2U question, I can't think of how you would getin the answer given those limits.
ah ok, thanksUnless it ends up being something like:
Then by subbing in the limits you would get that answer.
The source of this question isn't exactly known for strictly keeping questions 2U anyway. I'll just come back to it once we cover 3U methods then.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Bonus: Integrate that function, WITHOUT having first divided all terms by cos^2 (x).
But the questions says toBonus: Integrate that function, WITHOUT having first divided all terms by cos^2 (x).
lol we will just have to trust him on this oneBut the questions says to
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
I know it does, but I often promote 'alternative methods' to help build creativity with approaching problems (we are not sheep after all, are we?), which is often something valuable to have.But the questions says to
Here is an alternative way of doing the problem:

Thanks!  But how did you get from the first to second line? Partial fractions?
But how did you get from the first to second line? Partial fractions?
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Well, you could consider it to be 'partial fractions' I guess, but you can easily 'guess' what is supposed to be in the numerator.So you have to use partial fractions to get from the first to second line? Never used it for trig before
Here's what went on in my head:
1. The answer is ln(XXX), meaning that at some point I need to integrate something in the form f'(x)/f(x).
2. The only way I can get something in the form f'(x)/f(x) is if the top looks the same as the bottom, except with the functions swapped around (since derivative of sine is cos, and cos is - sine etc), so I just did that.
3. Oh look, a whole bunch of it cancels out if I cross multiply! But I also have a '6' lying around, so I'm going to chuck a 1/6 in front to 'balance' it out.
4. Good lord, it works out.
5. Add salt and pepper to season.
1. Yeah, I kept trying to look for that form as wellWell, you could consider it to be 'partial fractions' I guess, but you can easily 'guess' what is supposed to be in the numerator.
Here's what went on in my head:
1. The answer is ln(XXX), meaning that at some point I need to integrate something in the form f'(x)/f(x).
2. The only way I can get something in the form f'(x)/f(x) is if the top looks the same as the bottom, except with the functions swapped around (since derivative of sine is cos, and cos is - sine etc), so I just did that.
3. Oh look, a whole bunch of it cancels out if I cross multiply! But I also have a '6' lying around, so I'm going to chuck a 1/6 in front to 'balance' it out.
4. Good lord, it works out.
5. Add salt and pepper to season.
2. oooohh I see now. I forgot how convenient it is with sine/cosine lol
3-4. Yay!
5. rofl
Thanks
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Well, you could be smart and divide by cos2x then multiply by cos2x, then continue using Carrot's methodYes but...I want to know how you can do it the way the question specifies. Anyone got a solution?
too hard mateYes but...I want to know how you can do it the way the question specifies. Anyone got a solution?
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Wait...do you want a 2U method or a 3/4U method?Yes but...I want to know how you can do it the way the question specifies. Anyone got a solution?
If it's 3/4U, then after dividing, an appropriate substitution would be u = tan(x) and u' = sec2, therefore, the integrand becomes 1/ (9 - u2) which partial fractions can be applied or another appropriate method.
ahahaha, trueWell, you could be smart and divide by cos2x then multiply by cos2x, then continue using Carrot's method
yeah, that's was what nightweaver suggested before, and hopefully what I will learn soon.Wait...do you want a 2U method or a 3/4U method?
If it's 3/4U, then after dividing, an appropriate substitution would be u = tan(x) and u' = sec2, therefore, the integrand becomes 1/ (9 - u2) which partial fractions can be applied or another appropriate method.
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
You should, I mean, it's essential. Anyway, knowing it now would be a decent head-start, especially so you can focus on other topics which you might find harder.yeah, that's was what nightweaver suggested before, and hopefully what I will learn soon.
