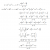-
Finished your HSC? Check out our University Discussion, Non-School forums or help out next year's HSC students! -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Infinite sum problem 1994 SGS (1 Viewer)
- Thread starter asianese
- Start date
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,256
- Gender
- Male
- HSC
- 2012
Don't know why my post isn't coming up- What I'm trying to say is you can only sum to inifinity like that if the absolute value of x is less than one and the question doesn't even ask for a summation to infinity, just n.
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,256
- Gender
- Male
- HSC
- 2012
No worries- its a relatively common mistake. An easy way to check something like that though is sub in some massive value like x=100. The LHS becomes huge but the RHS becomes tiny-> so you can easily conclude you made a mistake. For questions like this, always sub in something big though so the effect is even more obvious and you can confirm without a calc.
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,256
- Gender
- Male
- HSC
- 2012
Yep thats right so far. Now start a new G.P with x^2 as the first term, then another with x^3 as the first term etc. and sum them. They will all end on the same denominator and simplify nicely.i)
is all i got now
Godmode
Activated
Alrighty, brace for a complete mess; I have no idea how to use LaTex.
let S = x + 2x^2 + 3x^3 + ... + nx^n
now, xS = x^2 + 2x^3 + 3x^4 + ... + (n - 1)x^n + nx^(n+1)
subtracting xS from S, we get
S - xS = x + 2x^2 + 3x^3 + 4x^4 + ... + nx^n - (x ^2 + 2x^3 + 3x^4 + ... + (n - 1)x^n) - nx^(n+1)
after collecting like terms, we get
(1 - x)S = x + x^2 + x^3 + ... + x^n - nx^(n+1)
using the result from i. ,
(1 - x)S = x(x^n - 1)/(x -1) - nx^(n+1)
dividing through by (1 - x)
so S = x^(n + 1) - x/(x -1)(1 - x) - nx^(n+1)/(1 - x)
flipping the sign of the (1 -x) in the denominator,
S = nx^(n+1)/(x-1) - x^(n + 1)/(x - 1)^2 + x/(x - 1)^2
= [ n(x-1)x^(n+1) - x^(n+1) + x ]/(x - 1)^2
= [ nx^(n+2) - (n+1)x^(n+1) + x ] /(x-1)^2
therefore, x + 2x^2 + 3x^3 + ... + nx^n = [nx^(n + 2) - (n + 1)x^(n+1) + x]/(x-1)^2
just check my working, i may have made a mistake lol.
let S = x + 2x^2 + 3x^3 + ... + nx^n
now, xS = x^2 + 2x^3 + 3x^4 + ... + (n - 1)x^n + nx^(n+1)
subtracting xS from S, we get
S - xS = x + 2x^2 + 3x^3 + 4x^4 + ... + nx^n - (x ^2 + 2x^3 + 3x^4 + ... + (n - 1)x^n) - nx^(n+1)
after collecting like terms, we get
(1 - x)S = x + x^2 + x^3 + ... + x^n - nx^(n+1)
using the result from i. ,
(1 - x)S = x(x^n - 1)/(x -1) - nx^(n+1)
dividing through by (1 - x)
so S = x^(n + 1) - x/(x -1)(1 - x) - nx^(n+1)/(1 - x)
flipping the sign of the (1 -x) in the denominator,
S = nx^(n+1)/(x-1) - x^(n + 1)/(x - 1)^2 + x/(x - 1)^2
= [ n(x-1)x^(n+1) - x^(n+1) + x ]/(x - 1)^2
= [ nx^(n+2) - (n+1)x^(n+1) + x ] /(x-1)^2
therefore, x + 2x^2 + 3x^3 + ... + nx^n = [nx^(n + 2) - (n + 1)x^(n+1) + x]/(x-1)^2
just check my working, i may have made a mistake lol.
Godmode
Activated
No worries lol; one of these days, I swear I will learn LaTex.
Now I was wondering about the actual series in question, do we actually get the same result by summing each G.P. together? Or do we get another expression, and does it also tend to infinity? If they are different, which one 'grows' faster?
Now I was wondering about the actual series in question, do we actually get the same result by summing each G.P. together? Or do we get another expression, and does it also tend to infinity? If they are different, which one 'grows' faster?
Godmode
Activated
Haha I was thinking of that. That's how I got the idea behind my solution.
RealiseNothing
what is that?It is Cowpea
A pretty cool way:
}{x-1})
)
Now notice that the bit inside the bracket is the derivative of the first expression, so we find the derivative of the closed sum of the first expression:
}{x-1} = \frac{(x-1)(n+1)x^n - (x-1) - x(x^{n+1} - x)}{(x-1)^2})
Simplifying gives:
x^{n+1} - (n+1)x^n - (x-1) - x^{n+2} + x^2}{(x-1)^2})
Now we still have that 'x' out the front of the brackets from the second line, so lets multiply that in:
x^{n+2} - (n+1)x^{n+1} - x^2 + x + x^2 - x^{n+2}}{(x-1)^2})
Simplifying gives:
x^{n+1} + x}{(x-1)^2})
Which is the answer.
Now notice that the bit inside the bracket is the derivative of the first expression, so we find the derivative of the closed sum of the first expression:
Simplifying gives:
Now we still have that 'x' out the front of the brackets from the second line, so lets multiply that in:
Simplifying gives:
Which is the answer.
Last edited: