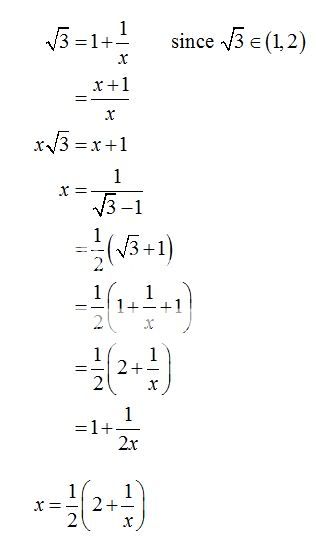I need help with this hard maths question (1 Viewer)

Stabilo123 · Feb 7, 2012

My brother asked me to do this question but I couldnt do it

1. Prove that Root 3 is irrational (pg 37 in Cambridge Yr 11 Book Question 4)

2. Prove the identity ( a + b + c )( ab + bc + ca ) - abc = ( a + b )( b + c )( c + a )

SpiralFlex · Feb 7, 2012

Common proof:

Assume $\sqrt{3}$ is rational.

Hence it can be expressed in the form,

$\sqrt{3}=\frac{p}{q}$

(Note: p, q have no common factors.)

Squaring,

$3=\frac{p^2}{q^2}$

$3q^2=p^2$

Clearly, $p^2$ is a multiple of $p,$ therefore so is $p.$

We can expressed this multiple of $3$ as,

$p=3k$

$(k \in \mathbb{Z})$

Substitute that in,

$3q^2=9k^2$

$q^2=3k^2$

$q^2$ is a multiple of 3! Hence so is $q$

Therefore we have just contradicted our assumption.

If both $p, q$ is a multiple of $3$ , it will have common factors.

$( a + b + c )( ab + bc + ca ) - abc = ( a + b )( b + c )( c + a )$

$LHS=a^2b+abc+a^2c+ab^2+b^2c+abc+abc+bc^2+ac^2-abc$

$=a^2b+2abc+a^2c+ab^2+b^2c+bc^2+ac^2....(2)$

$RHS=(ab+ac+b^2+cb)(c+a)$

$=abc+ac^2+b^2c+c^2b+a^2b+a^2c+ab^2+abc$

$=ab^2+2abc+ac^2+ab^2+b^2c + bc^2+ac^2$

$\therefore LHS=RHS$

Stabilo123 · Feb 7, 2012

thanks for doing the first one, but is there any way to do the 2nd one without just expanding both sides?

1xcv3we · Feb 7, 2012

I've given the 2nd one a shot by just expanding 1 side but to be honest with you this one has me stuck. Spiralflex's method is best method I know of if expanding then rearranging and factoring fails.

SpiralFlex · Feb 7, 2012

Stabilo123 said:
thanks for doing the first one, but is there any way to do the 2nd one without just expanding both sides?

From 2, I labelled. After expansion, of 2abc=abc+abc

$=c(ab+ac+b^2+cb)+a(ab+ac+b^2+cb)$

$=(a+c)(ab+ac+b^2+cb)$

AAEldar · Feb 7, 2012

$An alternate proof to SprialFlex's for the irrationality of $\sqrt{3}$.$

$Assume that $\sqrt{3}$ is rational, thereby being expressed in simplest form as:$

$\sqrt{3}=\frac{a}{b}$

$By squaring:$

$3=\frac{a^2}{b^2}$

$3b^2=a^2$

$$So, if $b$ is odd then so is $b^2$ and hence $a^2$ and $a$ are also odd. Similarly the same result applies if $b$ is even, but if this is the case then there is a common factor of $2$ and the ratio can be simplified more, contradicting our original statement so $a$ and $b$ must both be odd.$

$If this is the case, then we can express them as:$

$a=2p+1$

$b=2q+1$

$Where $p$ and $q$ are both integers. Substitute these expressions to obtain:$

$3(4q^2+4q+1)=4p^2+4p+1$

$6q^2+6q+1=2(p^2+p)$

$Now, the left hand side is always an odd integer but the right hand side is always an even integer. There is no solution to this line where an odd integer is equal to an even integer.$

$\therefore \sqrt{3}\neq \frac{a}{b}$ and hence is irrational.$$

Longer, but different.

SpiralFlex · Feb 7, 2012

^Very nice.

Carrotsticks · Feb 7, 2012

There is a faster way of doing the second question using something called 'Cyclic Expansion', which is a very useful tool sometimes. It eliminates the need for mindless and boring expansions.

Writing up an alternative proof for irrationality of sqrt3 now.

SpiralFlex · Feb 7, 2012

^Lol I like this method.

bleakarcher · Feb 7, 2012

Spiral, I dont really understand your common factors argument. Even if p and q had common factors they would cancel and leave still a rational number wouldnt they?

4025808 · Feb 7, 2012

I love the adding and subtraction of a value, it's such a smart manipulation technique

bladeys · Feb 7, 2012

I believe Carrotsticks wins

Carrotsticks · Feb 8, 2012

Here is a *rough* proof for irrationality of root 3.

Substituting x into itself recursively gives us an infinite periodic continued fraction, meaning that...

$\frac{1}{2} (\sqrt{3} + 1)$

... is irrational.

It follows through that the root of 3 is also irrational.

AAEldar · Feb 8, 2012

Different approach again - I like it though.

Trebla · Feb 8, 2012

bleakarcher said:
Spiral, I dont really understand your common factors argument. Even if p and q had common factors they would cancel and leave still a rational number wouldnt they?

The initial assumption is that p/q is the simplest fraction that the number can be. Perhaps a better worded version would be

$$Assume $\sqrt{3}=\dfrac{p}{q}\:$ where $p$ and $q$ are same sign integers with no common factors$\\\\\Rightarrow p^2 = 3q^2\\\\$Hence we can argue that $p^2$ is a multiple of $3$ given $q$ is an integer (hence so is $q^2$) but since $p$ is an integer then $p$ must be a multiple of $3$ as well because square numbers have repeated prime factors i.e. $p = 3k$ for some integer $k\\\\\Rightarrow 9k^2=3q^2\\\\\Rightarrow q^2=3k^2\\\\$Since $k$ is an integer (hence so is $k^2$) then by a similar argument $q = 3n$ for integer $n.\\\\$Thus, $p$ and $q$ have a common factor of $3$ which contradicts our initial assumption that $p$ and $q$ have no common factors. This implies that $\sqrt{3}$ cannot be written as a simplified fraction in the form $\dfrac{p}{q}$ hence it must be irrational$

Drongoski · Feb 8, 2012

Carrotsticks said:
There is a faster way of doing the second question using something called 'Cyclic Expansion', which is a very useful tool sometimes. It eliminates the need for mindless and boring expansions.

Writing up an alternative proof for irrationality of sqrt3 now.

If this is a Gawd's Method how about a Dawg's "Proof"?

Take any valid values for a, b and c chosen at random: for simplicity say a=1, b=2, c=-3

$\therefore (a+b)(b+c)(c+a) = (1+2)(2-3)(-3+1) = 6$

$(a+b+c)(ab+bc+ca) - abc = (1+2-3)(1 \times 2 - 1 \times 3 - 2 \times 3) - 1 \times 2 \times (-3) = 6$

Therefore RHS = LHS

Or, if you like, try any other values: say a = 2.37, b = 5.209 and c = 3.153

or you can use a Random Number Generator to furnish the 3 numbers.

PS:remember: (a+b)(b+c)(c+a) = (a+b+c)(ab+ac+ca) - abc is an identity.

Demento1 · Feb 8, 2012

Drongoski said:
If this is a Gawd's Method how about a Dawg's "Proof"?

Take any valid values for a, b and c chosen at random: for simplicity say a=1, b=2, c=-3

$\therefore (a+b)(b+c)(c+a) = (1+2)(2-3)(-3+1) = 6$

$(a+b+c)(ab+bc+ca) - abc = (1+2-3)(1 \times 2 - 1 \times 3 - 2 \times 3) - 1 \times 2 \times (-3) = 6$

Therefore RHS = LHS

Or, if you like, try any other values: say a = 2.37, b = 5.209 and c = 3.153

PS:remember: (a+b)(b+c)(c+a) = (a+b+c)(ab+ac+ca) - abc is an identity.

Exactly what I did for this question ^. I just let a,b and c all be integers and subbed and simplified it from there.

Carrotsticks · Feb 8, 2012

Demento1 said:
Exactly what I did for this question ^. I just let a,b and c all be integers and subbed and simplified it from there.

I'm not 100% sure if it constitutes a 'proof'.

SpiralFlex · Feb 8, 2012

Of course not haha.

Drongoski was merely demonstrating his puppy power!

Carrotsticks · Feb 8, 2012

SpiralFlex said:
puppy power!

wtf

I need help with this hard maths question (1 Viewer)

Member

Well-Known Member

Member

Undergraduate

Well-Known Member

Premium Member

Well-Known Member

Retired

Well-Known Member

Active Member

Well-Known Member

Member

Retired

Premium Member

Administrator

Well-Known Member

Philosopher.

Retired

Well-Known Member

Retired

Users Who Are Viewing This Thread (Users: 0, Guests: 1)