juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Let \;,A_{2}(x_{2},y_{2})\;,.......A_{n}(x_{n},y_{n})\;) be the only point to satisfying the hyperbola
be the only point to satisfying the hyperbola =c) and
and 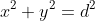
If and
and  . then
. then 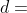
options
1,2,4,none
If
options
1,2,4,none
letbe the only point to satisfying the hyperbola
and
ifand
. Then
options
1,2,4,none
1Letbe the only point to satisfying the hyperbola
and
Ifand
. then
options
1,2,4,none
Letbe the only point to satisfying the hyperbola
and
Ifand
. then
options
1,2,4,none
I gave got the point that if hyperbola is tangent then there is only point of intersectiontry to sketch the two graphs meeting the constraints
Thanks for answerat the point (2 of them) of contact, y=x, the circle and the hyperbola are symmetrical about the line y=x, .: a=b
Sorry that I misled you. I wonder why my mistakes were not pointed out.Thanks for answer
but i did not understand if circle and Rectangular hyperbola are symmetrical about
then how can i get
and (ii) doubt is how we can say thatrepresent Rectangular Hyperbola
Sorry that I misled you. I wonder why my mistakes were not pointed out.
d^2=2a/(a+b) is ok. Points 0f contact of the 2 curves are at x=y=+/-sqrt(a/(a+b)), and gradient =-1.
Hence b=0 and d=sqrt2.
