Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC Mathematics Marathon (1 Viewer)
- Thread starter ohexploitable
- Start date
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Only because the question asked for induction. Its really just a repeated application of triangle's inequality.Well, technically it is. But still it's boring.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
"Hence" makes it easier
\\e^x \geq x^2+1)
Note that the integration step only works for x>=0
Note that the integration step only works for x>=0
Last edited:
- Joined
- Feb 16, 2005
- Messages
- 8,592
- Gender
- Male
- HSC
- 2006
There is a flaw in this approach. 2x > 2x is not true when 1 < x < 2Not worry about 'hence'
At
for
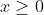
Thanks for that.There is a flaw in this approach. 2x > 2x is not true when 1 < x < 2
In that case, just drop 2^x in the inequality.
To justify e^x >2x: x=0, 1>0. d/dx of e^x = d/dx of 2x when x=ln2. When x=ln2, 2>2ln2. Since both are increasing, .: e^x>2x in [0,ln2]
For x>ln2, d/dx of e^x > d/dx of 2x, .: e^x>2x.
Last edited:
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
The result is correct, but this reasoning is rather incomplete.To justify e^x >2x: x=0, 1>0. d/dx of e^x = d/dx of 2x when x=ln2. When x=ln2, 2>2ln2. Since both are increasing, .: e^x>2x in [0,ln2]
For x>ln2, d/dx of e^x > d/dx of 2x, .: e^x>2x.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Try this approach:
Let f(x)=e^x-2x and show that f(x)>0 using simple calculus.
Let f(x)=e^x-2x and show that f(x)>0 using simple calculus.
Why is it incomplete?The result is correct, but this reasoning is rather incomplete.
How do you show that?Try this approach:
Let f(x)=e^x-2x and show that f(x)>0 using simple calculus.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
It is not immediate that this:Why is it incomplete?
"d/dx of e^x = d/dx of 2x when x=ln2.
When x=ln2, 2>2ln2."
justifies this:
"Since both are increasing, .: e^x>2x in [0,ln2]"
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
Similar to what you have tried to do but clearer. Just show the minimum of f(x) takes a positive value.How do you show that?
I thought I did that by pointing out at x=0, e^0>2(0).It is not immediate that this:
"d/dx of e^x = d/dx of 2x when x=ln2.
When x=ln2, 2>2ln2."
justifies this:
"Since both are increasing, .: e^x>2x in [0,ln2]"
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
The fact the relationship between the derivatives of the 2 functions don't change as x moves from 0 to ln2 is actually pretty vital in your argument.
The relationship does change. At x=0, d(e^x)/dx < d(2x)/dx. At x=ln2, they are the same.The fact the relationship between the derivatives of the 2 functions don't change as x moves from 0 to ln2 is actually pretty vital in your argument.
So I pointed out x=0, e^0>2(0) AND x=ln2, 2>2ln2.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
I mean in between 0 and ln2 (not inclusive of ln2), d(e^x)/dx < d(2x)/dx which is why your logic still works.The relationship does change. At x=0, d(e^x)/dx < d(2x)/dx. At x=ln2, they are the same.
So I pointed out x=0, e^0>2(0) AND x=ln2, 2>2ln2.
In general, the existence of changes in the relationship of derivatives of 2 functions can mean while they are still increasing functions, it is entirely possible for relationship between 2 functions to change as well, while still satisfying the other facts you have stated. Try constructing piecewise functions (still continuous though) which demonstrates this.
deterministic
Member
- Joined
- Jul 23, 2010
- Messages
- 423
- Gender
- Male
- HSC
- 2009
New questionThe locus of point P(x,y) is (x/2)^2+(y/b)^2=1, b>0. Find, in terms of b, the maximum value of x^2+2y.
hscishard
Active Member
Is it b^2 / 4 by any chance?

