leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: MX2 2016 Integration Marathon
So let's just clarify briefly that for this one, find the integral of e^(x)sin(x) and e^(x)cos(x) first using a 'loopy' integration by parts. Then, we use integration by parts on the given integral, treating x as the expression to be differentiated, then sub in our results immediately earlier.
You question skippersNEXT QUESTION:
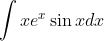
So let's just clarify briefly that for this one, find the integral of e^(x)sin(x) and e^(x)cos(x) first using a 'loopy' integration by parts. Then, we use integration by parts on the given integral, treating x as the expression to be differentiated, then sub in our results immediately earlier.

