KingOfActing
lukewarm mess
Re: HSC 2016 3U Marathon
Next question
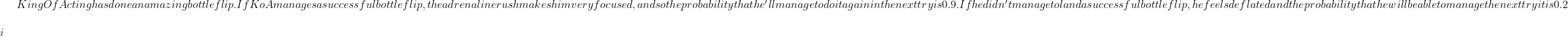 Let $ p_n$ be the probability of him successfully landing his $n$th bottle flip, with $p_0 = 1$. Find a relationship between $p_{n+1}$ and $p_n$.$\\\\$ii) Find the probability that flips his $100$th bottle successfully in exact form.$\\\\$iii) Suppose KingOfActing is a mythical being that will never die and will flip until time itself is over. What is the probability that he flips the last bottle in existence successfully? $)
Nah I remember it starts with "Let a + b + c = S" but I can't be bothered looking it up.Magically complete some squares?
Next question



