The first helpful thing to notice, is that the range of the cosine inverse function is between
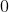
and
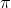
. This means we can't do the old method of cancelling out the inverse cosine and the cosine because this would give us
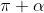
which since
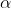
is acute would not be valid since it is outside the range.
However, we can still try to apply this by manipulating the expression. First, to give a proper definition of the trick, remember that:
 = x \ $for$ \ 0 \leq x \leq \pi \ (*))
This is true precisely because of the definition of an inverse function, and precisely because that domain
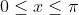
is the domain of the original
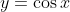
function that we wish to 'invert'.
So proceeding from this, we want to manipulate the given expression into one in which we can use
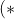 )
.
Remember that,
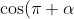 = -\cos \alpha )
and
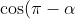 = - \cos \alpha )
, which means
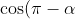 = \cos(\pi + \alpha) )
(To see this fact more clearly, imagine drawing horizontal lines in a y = cos x graph below the x-axis, and see that when the line intersects one part of the cosine graph, it intersects the opposite side,
symmetrical to
)
So that,
) = \cos^{-1} (\cos (\pi - \alpha)) )

) = \pi - \alpha \ $by using$ \ (*) )
) = \pi - \alpha )




