FrankXie
Active Member
Re: HSC 2014 4U Marathon - Advanced Level
ok here are the details. My previous calculation is for the case X, Y and theire wives all in one boat.
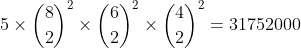
They can be in any of the five boates, which is why 5 times; 8 C 2 squared is for two men and two women chosen for the first boat of the remaining four boats; similarly for all other boats.
Now calculation for X and his wife in one boat and Y and his wife in the other boat (explanation quite similar so omitted)
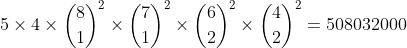
Therefore, total number of ways =31752000+508032000=539784000
ok here are the details. My previous calculation is for the case X, Y and theire wives all in one boat.
They can be in any of the five boates, which is why 5 times; 8 C 2 squared is for two men and two women chosen for the first boat of the remaining four boats; similarly for all other boats.
Now calculation for X and his wife in one boat and Y and his wife in the other boat (explanation quite similar so omitted)
Therefore, total number of ways =31752000+508032000=539784000
Last edited:

