funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 877
- Gender
- Male
- HSC
- 2010
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Basically we want to find the probability that all students have either 0, 1, or 2 oranges, and subtract that from 1 (complement etc).I got:
Which is basically 1.
If I understand your solution correctly, you're counting (*, O) as different to (O, *) where * is an orange, whereas these both correspond to a single orange for a single student (i.e. you'd be double-counting)Hence there are 30 places to put 20 oranges, so we can arrange this in the following amount of ways:
Right, I didn't take that into account.If I understand your solution correctly, you're counting (*, O) as different to (O, *) where * is an orange, whereas these both correspond to a single orange for a single student (i.e. you'd be double-counting)
My new answer is now:
Have no idea as to whether or not this is correct. I'm going to bed now though, I'll post my working out tomorrow. Basically if a person has either 0 or 2 oranges, they have not been double counted. So we consider the cases when a person has only been given 1 orange, and we use powers of 2 subtract 1, multipled by the amount of ways we choose this to get how many cases we double counted, then subtract from our total.
This probably makes no sense, I'm way too tired.
Unfortunately that integral evaluates to
Substituteinto the integral, which evaluates into
. Therefore since the integral is smaller than 2 and the sum is smaller than the integral, then the sum is smaller than 2.
Nice work.i)

ii)

Nice work.
================================

That looks right and it was a little different to my method, nice work, I think the sqrt 3 was supposed to be 3 sorry about that.
not sure if I'm on the right track, but does the answer happen to have a lot ofThat looks right and it was a little different to my method, nice work, I think the sqrt 3 was supposed to be 3 sorry about that.
=============
This is quite hard:
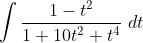
I don't think so, but I think its a bit unreasonable of me to ask it like that with no hint whatsoever.not sure if I'm on the right track, but does the answer happen to have a lot of?

