-
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012-14 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter bleakarcher
- Start date
- Status
- Not open for further replies.
FrankXie
Active Member
Re: MX2 Integration Marathon

which reduce the integral into via cancelling common factor, and
via cancelling common factor, and  via substitution
via substitution
but unfortunately partial fraction is still needed to solve these two
ok I reckon it is not a good question coz I hate partial fractions too. I wrote this question was to try using the techniqueI didn't forget, I just didn't bother. Any rational function can just be done by partial fractions, which isn't terribly exciting.
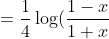+\frac{1}{2 \sqrt{3}}(\arctan(\frac{2x+1}{ \sqrt{3}})+\arctan(\frac{2x-1}{ \sqrt{3}}))+C.)
which reduce the integral into
but unfortunately partial fraction is still needed to solve these two
FrankXie
Active Member
Re: MX2 Integration Marathon

then notice that
\right]=\ln\frac2{1+\tan u}=\ln 2-\ln(1+\tan u) )
It follows that

which gives

hah, this is my favorite one. use substitution
then notice that
It follows that
which gives
dan964
what
Re: MX2 Integration Marathon
View attachment integral.pdf
edit: there is an error in the second last line. One of the pluses should be a minus. meh, who cares.
answer has been checked with WolframDont forget to try this one
View attachment integral.pdf
edit: there is an error in the second last line. One of the pluses should be a minus. meh, who cares.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
I would bet all my money, my house, my dog and my car that there is no elementary primitive.
Just saying.
I would bet all my money, my house, my dog and my car that there is no elementary primitive.
Just saying.
dan964
what
Re: MX2 Integration Marathon
which integral?I would bet all my money, my house, my dog and my car that there is no elementary primitive.
Just saying.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
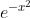
- Joined
- Feb 16, 2005
- Messages
- 8,631
- Gender
- Male
- HSC
- 2006
Re: MX2 Integration Marathon
Can you formally show that there is no elementary primitive?I would bet all my money, my house, my dog and my car that there is no elementary primitive.
Just saying.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
Whilst I'm aware of this theorem and the basic gist of it, I confess that I haven't had the opportunity to really dig into the meat of it.
Yep, you most certainly can.Can you formally show that there is no elementary primitive?
Whilst I'm aware of this theorem and the basic gist of it, I confess that I haven't had the opportunity to really dig into the meat of it.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
What makes the gamma function (for example) not elementary, but something like ln() or sin() elementary even though they are both transcendental?
Can you formally show that there is no elementary primitive?
Is there a rigorous definition of "elementary function"?Yep, you most certainly can.
Whilst I'm aware of this theorem and the basic gist of it, I confess that I haven't had the opportunity to really dig into the meat of it.
What makes the gamma function (for example) not elementary, but something like ln() or sin() elementary even though they are both transcendental?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
Elementary function = anything formed recursively (using the operations of +,-,*,/,^ and composition) from: the reals, the monomial x, the 3 trig funcs and their inverses, the 3 hyp trig funcs and their inverses, the exponential and the logarithm.
I don't know that theres any universally agreed upon definition though, its not particularly important because its just a matter of conventions.
I would say something likeIs there a rigorous definition of "elementary function"?
What makes the gamma function (for example) not elementary, but something like ln() or sin() elementary even though they are both transcendental?
Elementary function = anything formed recursively (using the operations of +,-,*,/,^ and composition) from: the reals, the monomial x, the 3 trig funcs and their inverses, the 3 hyp trig funcs and their inverses, the exponential and the logarithm.
I don't know that theres any universally agreed upon definition though, its not particularly important because its just a matter of conventions.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
The standard definition is a function that can be constructed via a finite number of applications of roots (of degree n, tbh I don't remember if n had to be rational), exponentiations and logarithms under your elementary operations (hence the name) and compositions. With enough playing around (using the fact that we can construct the trigs using complex exponentials), then we've also got the trigs and inverse trigs thrown in there too. The gamma function isn't considered elementary I presume it cannot be constructed using a finite number of 'allowed' things I've listed. As for the proof of that, I am not too sure to be honest. I've not yet had a proper look into that.
EDIT: Beaten.
The standard definition is a function that can be constructed via a finite number of applications of roots (of degree n, tbh I don't remember if n had to be rational), exponentiations and logarithms under your elementary operations (hence the name) and compositions. With enough playing around (using the fact that we can construct the trigs using complex exponentials), then we've also got the trigs and inverse trigs thrown in there too. The gamma function isn't considered elementary I presume it cannot be constructed using a finite number of 'allowed' things I've listed. As for the proof of that, I am not too sure to be honest. I've not yet had a proper look into that.
EDIT: Beaten.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
Thinking about it a bit more carefully now, the question "What makes a function elementary" is a lot more complicated than at first glance. I'm even getting a little confused regarding the definition I've learned (finite applications of etc). Asking myself questions like is an integral constructed via an infinite sum elementary? Is a function produced using the infinite geometric sum not elementary then? How about strange numbers like Liouville's Constant? Roots of polynomials of degree 5 or more?
Thinking about it a bit more carefully now, the question "What makes a function elementary" is a lot more complicated than at first glance. I'm even getting a little confused regarding the definition I've learned (finite applications of etc). Asking myself questions like is an integral constructed via an infinite sum elementary? Is a function produced using the infinite geometric sum not elementary then? How about strange numbers like Liouville's Constant? Roots of polynomials of degree 5 or more?
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
I'm pretty sure all constant functions are considered elementary, no matter how unusual the number. (Most numbers are transcendental anyway, which imo is weirder than being a root of a poly that cant be expressed by radicals).
Also, the recursive building of an elementary function from the "building blocks" has to be finite. Then you can study this thing as an algebraic object using Galois theory. (Which is how you prove that certain things don't have elementary primitives).
So no, infinite sums/products don't count. Otherwise we are opening the gates for pretty much all the special functions.
I'm pretty sure all constant functions are considered elementary, no matter how unusual the number. (Most numbers are transcendental anyway, which imo is weirder than being a root of a poly that cant be expressed by radicals).
Also, the recursive building of an elementary function from the "building blocks" has to be finite. Then you can study this thing as an algebraic object using Galois theory. (Which is how you prove that certain things don't have elementary primitives).
So no, infinite sums/products don't count. Otherwise we are opening the gates for pretty much all the special functions.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
Where I am not sure is when you consider things like Taylor Series for say the sine function. The sine function is most certainly elementary yet the Taylor Series is of course infinite, so it cannot be elementary?? This is where I'm not completely sure.I'm pretty sure all constant functions are considered elementary, no matter how unusual the number. (Most numbers are transcendental anyway, which imo is weirder than being a root of a poly that cant be expressed by radicals).
Also, the recursive building of an elementary function from the "building blocks" has to be finite. Then you can study this thing as an algebraic object using Galois theory. (Which is how you prove that certain things don't have elementary primitives).
So no, infinite sums/products don't count. Otherwise we are opening the gates for pretty much all the special functions.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
sin(x) can be obtained by applying absolutely 0 operations as it is itself one of the basic functions. Hence it is elementary.
The word "can" is key. The fact that it can also be written as an everywhere convergent infinite series as well is irrelevant. Otherwise the function 1/(1-x) on |x|<1 would have to be excluded as well, as it is the sum of the geometric series.
In fact all of the elementary functions are nice enough to be analytic on their appropriate domains I think.
Well the precise defn would be: CAN be obtained by a finite recursive application of the allowed operations on the listed basic functions.Where I am not sure is when you consider things like Taylor Series for say the sine function. The sine function is most certainly elementary yet the Taylor Series is of course infinite, so it cannot be elementary?? This is where I'm not completely sure.
sin(x) can be obtained by applying absolutely 0 operations as it is itself one of the basic functions. Hence it is elementary.
The word "can" is key. The fact that it can also be written as an everywhere convergent infinite series as well is irrelevant. Otherwise the function 1/(1-x) on |x|<1 would have to be excluded as well, as it is the sum of the geometric series.
In fact all of the elementary functions are nice enough to be analytic on their appropriate domains I think.
Last edited:
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: MX2 Integration Marathon
Funny you mention that specific geometric sum, I was thinking precisely that to put in my previous post, but decided to use the Taylor Series example to avoid any potential for the radius of convergence playing some role somehow.
Cheers, that's what I was looking for.Well the precise defn would be: CAN be obtained by a finite recursive application of the allowed operations on the listed basic functions.
sin(x) can be obtained by applying absolutely 0 operations as it is itself one of the basic functions. Hence it is elementary.
The word "can" is key. The fact that it can also be written as an everywhere convergent infinite series as well is irrelevant. Otherwise the function 1/(1-x) on |x<1| would have to be excluded as well, as it is the sum of the geometric series.
Funny you mention that specific geometric sum, I was thinking precisely that to put in my previous post, but decided to use the Taylor Series example to avoid any potential for the radius of convergence playing some role somehow.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
Its a pretty nice and simple sum lol.Cheers, that's what I was looking for.
Funny you mention that specific geometric sum, I was thinking precisely that to put in my previous post, but decided to use the Taylor Series example to avoid any potential for the radius of convergence playing some role somehow.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
What if I say
Elementary = anything formed recursively (using the operations of +,-,*,/,^ and composition) from: the reals, the monomial x, the 3 trig funcs and their inverses, the 3 hyp trig funcs and their inverses, the exponential and the logarithm, AND the Gamma function
Is there a reason why my this addition to the definition is wrong? Is the concept of elementary functions purely a categorization of mathematicians?
I would say something like
Elementary function = anything formed recursively (using the operations of +,-,*,/,^ and composition) from: the reals, the monomial x, the 3 trig funcs and their inverses, the 3 hyp trig funcs and their inverses, the exponential and the logarithm.
I don't know that theres any universally agreed upon definition though, its not particularly important because its just a matter of conventions.
Is there a reason for that specific list of functions to be considered elementary?Well the precise defn would be: CAN be obtained by a finite recursive application of the allowed operations on the listed basic functions.
sin(x) can be obtained by applying absolutely 0 operations as it is itself one of the basic functions. Hence it is elementary.
The word "can" is key. The fact that it can also be written as an everywhere convergent infinite series as well is irrelevant. Otherwise the function 1/(1-x) on |x|<1 would have to be excluded as well, as it is the sum of the geometric series.
In fact all of the elementary functions are nice enough to be analytic on their appropriate domains I think.
What if I say
Elementary = anything formed recursively (using the operations of +,-,*,/,^ and composition) from: the reals, the monomial x, the 3 trig funcs and their inverses, the 3 hyp trig funcs and their inverses, the exponential and the logarithm, AND the Gamma function
Is there a reason why my this addition to the definition is wrong? Is the concept of elementary functions purely a categorization of mathematicians?
dan964
what
- Status
- Not open for further replies.
