-
Best of luck to the class of 2024 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here -
YOU can help the next generation of students in the community! Share your trial papers and notes on our Notes & Resources page
iii)
v)
x = 1 is a trivial vertical asymptote because plugging in x = 1 gives 1/0 which is undefined..
It might be a good idea to go over the theory for the chapter.
I'll give a quick summary for part 3 to help you along:
Horizontal asymptotes occur when a graph tends to a particular value for extremely large values of ‘x’.
In the question given, y=0 is a horizontal asymptote because for larger and larger values of x (eg 100000), the answer will be closer and closer to 0 (i.e. y=0). Similarly for larger and larger values of negative x (eg -1000000).
Here's a quick hack to find horizontal asymptotes for harder questions:
Hack #1: When you just care about finding horizontal asymptotes, use your calculator to sub in 10, then sub in 100, then sub in 1000. is the answer getting closer and closer to something? that's more likely than not a horizontal asymptote.
Hack #2: A slightly more algebraic way is to substitute in f(∞), and see what happens.
To illustrate, let's consider 3 possible cases:
1.
If =\frac{\left( 2x^2+x+1 \right)}{\left( 3x^2+7 \right)})
, then:  =\frac{\left( 2\left( \infty \right) ^2+\infty +1 \right)}{\left( 3\left( \infty \right) ^2+7 \right)})
Now, when we’re dealing with infinity squared, infinity and constants might as well not exist. For example, if you had infinity plus one, does the one here make a difference? No... the 'one' is insignificant really, and you will still have infinity. Similarly, when you have infinity squared, then even infinity is insignificant... it is an infinite times smaller than infinity squared. therefore, we can disregard it (for the purposes of this hack ;p)
So really, we’re dealing with: =\frac{2\left( \infty \right) ^2}{3\left( \infty \right) ^2})
.
And now the two infinity squares will 'clearly' cancel each other out, leaving us with 2/3. That is, as x approaches ±∞, f(x) will approach 2/3. So our horizontal asymptote is: y=2/3.
2.
If =\frac{\left( 7+5x^2+4x^3 \right)}{\left( x^4+2 \right)})
, then:  =\frac{\left( 7+5\left( \infty \right) ^2+4\left( \infty \right) ^3 \right)}{\left( \left( \infty \right) ^4+2 \right)})
Again, we’re really dealing with: =\frac{\left( 4\left( \infty \right) ^3 \right)}{\left( \infty \right) ^4})
, but here, after cancelling, we have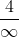 
.
4 divided by infinity will be 0, therefore as x approaches ±∞, f(x) will approach 0. H.A. is therefore y=0.
3.
If =\frac{\left( x^3-2 \right)}{\left( 1+x^2 \right)})
, then:  =\frac{\left( \left( \infty \right) ^3-2 \right)}{\left( 1+\left( \infty \right) ^2 \right)})
Lastly, if the top is infinitely bigger, then of course there is no horizontal asymptote as we have a very big number divided by a small number. We’re really dealing with =\frac{\left( \infty \right) ^3}{\left( \infty \right) ^2})
, but after cancelling, we’re left with: f(∞)=∞, which means there’s no asymptote. It will keep increasing until infinity!
tl;dr summary:
1. Consider the terms with the highest powers in both the numerator and the denominator. Disregard all other terms.
2. If the power of the numerator term is greater, there is no H.A.
3. If the power of the denominator term is greater, H.A. is at y=0 (i.e. x-axis).
4. If the powers are equal, H.A. will be:
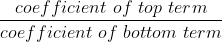
(Technicality, while oblique asymptotes exist, you don't need to worry about them in 2u afaik. The above summary will serve you fine.)
Note: most competent math nerds are prolly squirming over how un-mathy the above is lel.
But once you get the above, you should be able to understand the correct way to approach the whole topic, which should be in your textbook.
btw, latex is bloody annoying.
I'll give a quick summary for part 3 to help you along:
Horizontal asymptotes occur when a graph tends to a particular value for extremely large values of ‘x’.
In the question given, y=0 is a horizontal asymptote because for larger and larger values of x (eg 100000), the answer will be closer and closer to 0 (i.e. y=0). Similarly for larger and larger values of negative x (eg -1000000).
Here's a quick hack to find horizontal asymptotes for harder questions:
Hack #1: When you just care about finding horizontal asymptotes, use your calculator to sub in 10, then sub in 100, then sub in 1000. is the answer getting closer and closer to something? that's more likely than not a horizontal asymptote.
Hack #2: A slightly more algebraic way is to substitute in f(∞), and see what happens.
To illustrate, let's consider 3 possible cases:
1.
If
Now, when we’re dealing with infinity squared, infinity and constants might as well not exist. For example, if you had infinity plus one, does the one here make a difference? No... the 'one' is insignificant really, and you will still have infinity. Similarly, when you have infinity squared, then even infinity is insignificant... it is an infinite times smaller than infinity squared. therefore, we can disregard it (for the purposes of this hack ;p)
So really, we’re dealing with:
And now the two infinity squares will 'clearly' cancel each other out, leaving us with 2/3. That is, as x approaches ±∞, f(x) will approach 2/3. So our horizontal asymptote is: y=2/3.
2.
If
Again, we’re really dealing with:
4 divided by infinity will be 0, therefore as x approaches ±∞, f(x) will approach 0. H.A. is therefore y=0.
3.
If
Lastly, if the top is infinitely bigger, then of course there is no horizontal asymptote as we have a very big number divided by a small number. We’re really dealing with
tl;dr summary:
1. Consider the terms with the highest powers in both the numerator and the denominator. Disregard all other terms.
2. If the power of the numerator term is greater, there is no H.A.
3. If the power of the denominator term is greater, H.A. is at y=0 (i.e. x-axis).
4. If the powers are equal, H.A. will be:
(Technicality, while oblique asymptotes exist, you don't need to worry about them in 2u afaik. The above summary will serve you fine.)
Note: most competent math nerds are prolly squirming over how un-mathy the above is lel.
But once you get the above, you should be able to understand the correct way to approach the whole topic, which should be in your textbook.
btw, latex is bloody annoying.
Last edited:
A much more rigorous approach is possible with fractions made of polynomials, involving dividing by the (monic) term with highest power of x in the denominator and then using the fact that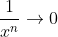 
as 
for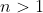 
.
Example 1:
 = \frac{2x^2 + x + 1}{3x^2 + 7} = \cfrac{\frac{2x^2}{x^2} + \frac{x}{x^2} + \frac{1}{x^2}}{\frac{3x^2}{x^2} + \frac{7}{x^2}} = \cfrac{2 + \frac{1}{x} + \frac{1}{x^2}}{3 + \frac{7}{x^2}})
So, = \lim_{x \to \infty} \cfrac{2 + \frac{1}{x} + \frac{1}{x^2}}{3 + \frac{7}{x^2}} = \cfrac{2 + 0 + 0}{3 + 0} = \frac{2}{3})
So,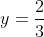
is a horizontal asymptote for 
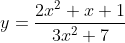as .
Example 2:
 = \frac{7 + 5x^2 + 4x^3}{x^4 + 2} = \cfrac{\frac{7}{x^4} + \frac{5x^2}{x^4} + \frac{4x^3}{x^4}}{\frac{x^4}{x^4} + \frac{2}{x^4}} = \cfrac{\frac{7}{x^4} + \frac{5}{x^2} + \frac{4}{x}}{1 + \frac{2}{x^4}})
So, = \lim_{x \to \infty} \cfrac{\frac{7}{x^4} + \frac{5}{x^2} + \frac{4}{x}}{1 + \frac{2}{x^4}} = \cfrac{0 + 0 + 0}{1 + 0} = 0)
So, the x-axis is a horizontal asymptote for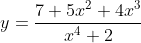
as .
Example 3:
 = \frac{x^3 - 2}{1 + x^2} = \cfrac{\frac{x^3}{x^2} - \frac{2}{x^3}}{\frac{1}{x^2} + \frac{x^2}{x^4}} = \cfrac{x - \frac{2}{x^3}}{\frac{1}{x^2} + 1})
So, = \lim_{x \to \infty} \cfrac{x - \frac{2}{x^3}}{\frac{1}{x^2} + 1} = \cfrac{x - 0}{1 + 0} \to x)
So,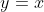
is a diagonal asymptote for 
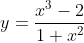as .
Example 1:
So,
So,
Example 2:
So,
So, the x-axis is a horizontal asymptote for
Example 3:
So,
So,
Last edited: