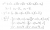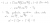For question 2 we are given
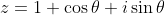
The modulus requires us to find
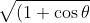^{2}+\sin^{2}\theta} = \sqrt{2+2\cos{\theta}})
. Now notice that you need to use the double angle formula to notice that
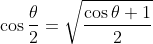
. Multiply by 2 and you will have
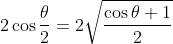
. Now 2 is just the square root of 4 right, so therefor multiply the RHS your modulus is just
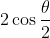
.
Since we are also finding the argument one important note is that for a complex number to be written in the modulus-argument form it will be written in the form of
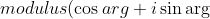)
. Remember we have
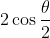
as our modulus.
The argument will come from the structure of the complex number.
See here
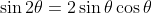
Well in that case you can clearly see that
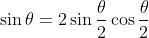
.
Using the double angle formula
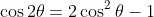
then it is obvious that
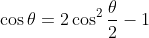
and
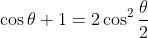
now if we are finding the mod arg form then it becomes
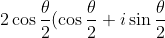)
Thus your final answer will be that the argument is

This part simply asks you to do this convert
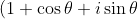^{n})
into mod arg form which we have found and then apply De Moivre's Theorem. Easy as cake.
part ii starts off asking us to use the real part of the complex number and combining De Moivre's Theorem and Binomial Theorem we will have
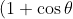^{4}=1+4\cos{\theta}+6\cos^{2}{\theta}+4\cos^{3}{\theta}+\cos^{4}{\theta})
. As noticed for the modulus argument form we will also take the real part of the complex number giving us
^{4})
. Now as noted the modulus part when you raise to the power of 4 it gives us
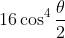
and for the argument part we use De Moivre's Theorem which will give us
 = \cos{2\theta})
. Once you have that you can clearly see that from the question
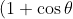^{4} = 16\cos^{4}{\frac{\theta}{2}} \cos{2\theta})
giving us
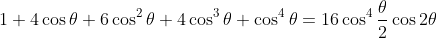
.