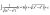-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Help me prove this standard form please (1 Viewer)
- Thread starter WEMG
- Start date
Aquawhite
Retiring
Are you only interested in how to do the proof, because it is given to you on the standard integrals sheet and hence won't have to know the proof or know the conversation by heart... just how to use it.
Sorry, I don't actually know the proof though.
Sorry, I don't actually know the proof though.
For integral to end up with that expression means if you differentiate w.r.t. x that expression you should get back the integrand: 1/sqrt(x^2 - a^2)
which you indeed will thus: d/dx[ln{x + sqrt(a^2-a^2)}] =
(1/x + sqrt(x^2 - a^2)) . [1 + 0.5(x^2 - a^2)^[-0.5] .2x] = the integrand
So this means, if you like, you can reverse this process to get the derivation for the integral formula.
That is - you have a proof.
EDIT: I've forgotten how to & I'm too dumb to figure out how/where I can access the LaTeX facility.
Can someone help out so I can post in LaTeX again. Or do I need to go back to using TeX
Last edited:
Pwnage101
Moderator
1).Use the substituion x=a(sec(u))
2). To integrate sec(u) with respect to u note that d/du{sec(u)+tan(u)}=sec(u)[sec(u)+tan(u)], hence multiplying sec(u) by {sec(u)+tan(u)}/{sec(u)+tan(u)} will make things nice.
3). To transform the result from the variable u to x, draw up a right angled triangle
4). Use log-laws to reduce the expression so that all constants (i.e. terms that do not involve x) come under the constant of integration
Have a go. If you're still stuck, i'm sure many will help further.
2). To integrate sec(u) with respect to u note that d/du{sec(u)+tan(u)}=sec(u)[sec(u)+tan(u)], hence multiplying sec(u) by {sec(u)+tan(u)}/{sec(u)+tan(u)} will make things nice.
3). To transform the result from the variable u to x, draw up a right angled triangle
4). Use log-laws to reduce the expression so that all constants (i.e. terms that do not involve x) come under the constant of integration
Have a go. If you're still stuck, i'm sure many will help further.
jet
Banned
- Joined
- Jan 4, 2007
- Messages
- 3,148
- Gender
- Male
- HSC
- 2009
Depends really. IMO they require about the same amount of work. Once you integrate you still need to convert from the inverse trig form to logarithmic form.It's easier if you use hyperbolic functions. But that's 1st year uni material.