Harder rates of change (1 Viewer)

[asianese]

It may be from 3U Fitzpatrick but I'm not sure

A rectangular vessel is divided into 2 equal compartments by a vertical porous membrane. Liquid in one compartment, initially at a depth of 20cm, passes into the other compartment, initially empty, at a rate proportional to the difference in the levels.

a) If the depth of liquid in one of the vessels at any time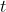 is , show that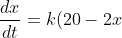
b) Show that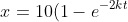
c) If the level in the originally empty compartment rises 2cm in the first 5 minutes, after what time difference will the difference in the levels be 2cm?

Please help with c).

Thankyou!

 

[Aesytic]

subbing the information into the equation you showed in b),
2 = 10(1-e^(-2*5*k))
1/5 = 1 - e^(-10k)
e^(-10k) = 4/5
-10k = ln(4/5)
.'. k = -(ln(4/5))/10

when the difference in water level is 2cm, then 20-x - x = 2, since the level of the water in the compartment which initially had 20cm will now have 20-x cm, and the other compartment will have x cm
.'. 20-2x = 2
10-x = 1
x = 9

subbing back into the equation we found in b)
9 = 10(1 - e^(-2*(-ln(4/5)/5)*t)), because we found the value of k from before
9/10 = 1-e^((ln(4/5)/5)*t)
= 1 - (4/5)^(t/5)
(4/5)^(t/5) = 1/10
t/5 = log base 4/5 of (1/10)
.'. t = 5*[log base 4/5 of (1/10)]

i might've made a mistake somewhere, but hopefully you get the method of doing it