From i) we know that:
g(x)dx]^{2} \leq \int_{0}^{a}[f(x)]^{2}dx\int_{0}^{a}[g(x)]^{2}dx)
if we let:
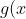=a=1)
into the above inequality we get:
dx]^{2} \leq \int_{0}^{1}[f(x)]^{2}dx\int_{0}^{1}1^{2}dx)
which simplifies to:
dx]^{2} \leq \int_{0}^{1}[f(x)]^{2}dx)
and now part ii) is done.
For part iii) first we square the inequality from ii) to get:
dx]^{4} \leq [\int_{0}^{1}[f(x)]^{2}dx]^2)
So now to finish this question we have to prove that:
]^{2}dx]^2\leq \int_{0}^{1}[f(x)]^{4}dx)
To do this we let:
=a=1, g(x)=[f(x)]^{2})
for part i, which gives us:
]^{2}dx]^{2} \leq \int_{0}^{1}[1]^{2}dx\int_{0}^{1}[(f(x))^{2}]^{2}dx)
this simplifies to:
]^{2}dx]^{2} \leq \int_{0}^{1}[f(x)]^{4}dx)
so now we sub this result into:
dx]^{4} \leq [\int_{0}^{1}[f(x)]^{2}dx]^2)
which yields:
dx]^{4}\leq \int_{0}^{1}[f(x)]^{4}dx)
and we are done.
For part iii) we couldn't let:
=[f(x)]^{2})
as this obviously looks stupid, so we let f(x)=1 and
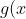=[f(x)]^{2})
as mentioned above