Hi~
I'm getting stuck on drawing graphs of derivative functions, and was wondering if someone could be sweet enough to tell me what the graph of a derivative function would look like when its primitive has a turning point and stationary point. Also the attached image - did I draw it right?
Thanks C: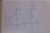
I'm getting stuck on drawing graphs of derivative functions, and was wondering if someone could be sweet enough to tell me what the graph of a derivative function would look like when its primitive has a turning point and stationary point. Also the attached image - did I draw it right?
Thanks C:




