Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
'Game Theory' on Coursera (Jan 7 - Feb 25) (1 Viewer)
- Thread starter OzKo
- Start date
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
I feel posting here isn't violating my bostirement too badly. How is everyone finding the course? I got 9 for the first week but I had looked at similar things to that weeks material before. About to look at this weeks stuff.
OzKo
Retired
- Joined
- Jul 17, 2007
- Messages
- 9,892
- Gender
- Male
- HSC
- 2009
- Uni Grad
- 2013
I'm finding it fairly challenging myself.I feel posting here isn't violating my bostirement too badly. How is everyone finding the course? I got 9 for the first week but I had looked at similar things to that weeks material before. About to look at this weeks stuff.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Nope, sign up now. Its only been running for a week.Is it too late to try this out? Didn't see this thread early but 'game theory' is something I guess I wanna learn a bit I dunno, probably because it was talked alot about in the TV series numb3rs =/.
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Some cool 'challenge' maths questions I came up with:
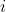 In a 2 player game where $|A_1| = n$, $|A_2| = m$, and all payoff values are distinct, show that there can be no more than $\min(n,m)$ Nash equilibria.)
 You are now given that $n = m$, and furthermore that there are precisely $n$ Nash equilibria. Call a cell of the payoff matrix \textbf{red} if it is represents a Nash equilibrium and \textbf{blue} otherwise. Find the number of distinct possible colourings of the payoff matrix.$)
 Show that the answer to part ii) is at least as large as the number of ways one can place 8 queens on a chessboard so that no two queens attack each other.$)
And a compsci question too:
$ algorithm for identifying all Nash equilibria.$)
And a compsci question too:
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Sure about the first question? What about the game with payoff (0,0) for each strategy profile? That has exactly mn equilibria.Some cool 'challenge' maths questions I came up with:
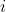 In a 2 player game where $|A_1| = n$ and $|A_2| = m$, show that there can be no more than $\min(n,m)$ Nash equilibria.)
And a compsci question too:
$ algorithm for identifying all Nash equilibria.$)
GoldyOrNugget
Señor Member
- Joined
- Jul 14, 2012
- Messages
- 577
- Gender
- Male
- HSC
- 2012
Whoops, edited. I'm not sure about any of the questionsSure about the first question? What about the game with payoff (0,0) for each strategy profile? That has exactly mn equilibria.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Well the payoff corresponding to each action profile is a 2-vector of reals, saying that they are all distinct doesn't mean that they cannot still have one component equal, wherein lies the problem.
(2,1)|(1,1)
-----------
(2,2)|(1,2)
for instance has all action profiles as pure strat Nash equilibria. If you meant (as I am guessing you did) that every element of every payoff vector is distinct, then the key idea is that we cannot have two Nash equilibria in any row or column (as one would be preferred by the player whose action set give rise to the row or column).
And your colourings correspond to permutations of the set {1,2,...,n}, of which there are exactly n!.
The each colouring is equivalent to placing n rooks on an nxn chessboard in such a way that no two are attacking each other. From this observation iii) is clear.
(2,1)|(1,1)
-----------
(2,2)|(1,2)
for instance has all action profiles as pure strat Nash equilibria. If you meant (as I am guessing you did) that every element of every payoff vector is distinct, then the key idea is that we cannot have two Nash equilibria in any row or column (as one would be preferred by the player whose action set give rise to the row or column).
And your colourings correspond to permutations of the set {1,2,...,n}, of which there are exactly n!.
The each colouring is equivalent to placing n rooks on an nxn chessboard in such a way that no two are attacking each other. From this observation iii) is clear.
OzKo
Retired
- Joined
- Jul 17, 2007
- Messages
- 9,892
- Gender
- Male
- HSC
- 2009
- Uni Grad
- 2013
Ended up stopping in the end because of laziness.Sorry to bump an old thread but I was just wondering how you all went/if you ended up completing it, and if so was it worth it?
That being said, the course was well designed from what I saw of it.
nerdasdasd
Dont.msg.me.about.english
Would these courses be considered on your cv?
Just had a look at that myself, most people say it's worth putting on but in terms of giving you an edge it's nothing huge.Would these courses be considered on your cv?
Thanks for thatEnded up stopping in the end because of laziness.
That being said, the course was well designed from what I saw of it.

