KingOfActing
lukewarm mess
So in my boredom these holidays I have thought up the following functional equation:
 = \frac{1}{f(x)})
With the only restriction being that it is continuous on .
.
I first looked at constant solutions, which gave me = \pm 1)
Then linear solutions were all = \pm x)
And in general, any polynomial solution is = \pm x^n) for some natural n. Just through inspection it becomes clear that this works for any real n.
for some natural n. Just through inspection it becomes clear that this works for any real n.
I then went on to try rational functions, and after solving for general linear/linear and quadratic/quadratic, I noticed the pattern that the general rational function which is a solution to this functional equation is of the form = \pm \frac{a_0x^n+a_1x^{n-1}+...+a_n}{a_nx^n+a_{n-1}x^{n-1}+...+a_0}) . This solution also includes all previous solutions as well.
. This solution also includes all previous solutions as well.
I've also found:
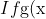$ is a solution, then so is $ \frac{1}{g(x)}\\$If $g(x)$ and $h(x)$ are both solutions, then so is $g(x)h(x)\\f(1) = \pm 1\\f(-1) = \pm 1)
Is there any more general form for the solution than the one I've found? Any transcendental functions/non-elementary functions that satisfy the equation?
With the only restriction being that it is continuous on
I first looked at constant solutions, which gave me
Then linear solutions were all
And in general, any polynomial solution is
I then went on to try rational functions, and after solving for general linear/linear and quadratic/quadratic, I noticed the pattern that the general rational function which is a solution to this functional equation is of the form
I've also found:
Is there any more general form for the solution than the one I've found? Any transcendental functions/non-elementary functions that satisfy the equation?

