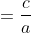Demento's Year 10 maths practice paper thread (7 Viewers)

[SpiralFlex]

I really cbf'd getting them to prove it right now. I started making that question at 9:50, finished it at 11:35 or something. Just relaxing now lol.

Meanie, that's like pushing a child into a pool of sharks.

 

[HSC2014]

It was a test. How can I check the solutions?! lol

I was talking about your solutions to the abs value questions. If you did them by case definitions, then you have to check their met the conditions (If you don't get what I'm saying dw. And there was only 20 questions all together so probably wasn't too many abs values).

 

[Sy123]

Introduction to Realise's question:

i) Given that




and



Prove that:







Then continue with realise's question.

 

[Demento1]

Introduction to Realise's question:

i) Given that



and



Prove that:






Then continue with realise's question.

Will give this a go tomorrow - looking forward to it. Goodnight guys (or morning).

 

[SpiralFlex]

Introduction to Realise's question:

i) Given that



and



Prove that:






Then continue with realise's question.

Defining alpha and beta as the roots of course.

 

[Fawun]

Introduction to Realise's question:

i) Given that



and



Prove that:






Then continue with realise's question.

What the heck how does ax^2 + bx + c turn out to be (x-a)(x-b)

:S

 

[HSC2014]

SpiralFlex, aren't you meant to be studying 24/7 for HSC t_t

 

[Sy123]

Defining alpha and beta as the roots of course.

Oh yes, of couse lol.

What the heck how does ax^2 + bx + c turn out to be (x-a)(x-b)

:S

well ax^2+bx+c=0.

Do something to the x^2 term (and hence the whole expression) to get it into a desirable form in order to then utilise the equivalence to (x-alpha)(x-beta)

 

[RealiseNothing]

What the heck how does ax^2 + bx + c turn out to be (x-a)(x-b)

:S

When you expand the brackets.....

 

[SpiralFlex]

When you expand the brackets.....

You guys need to give her a bit of context

 

[SpiralFlex]

SpiralFlex, aren't you meant to be studying 24/7 for HSC t_t

BOS 24/7, screw HSC! I got centrelink!

 

[SpiralFlex]

So no one is going to explain to Fawn? If not I have to then...(eating my pie)

 

[Fawun]

Oh yes, of couse lol.



well ax^2+bx+c=0.

Do something to the x^2 term (and hence the whole expression) to get it into a desirable form in order to then utilise the equivalence to (x-alpha)(x-beta)

idgi

but maybe that's because it's like 12:30am and my brain isn't functioning properly

When you expand the brackets.....

Yes because the LHS looks the same as the RHS

 

[twinklegal19]

Yes because the LHS looks the same as the RHS

they don't have to, that's why it says "equivalent to" rather than the usual equals sign. We're just establishing the fact that they are identical to each other if that makes sense

(sorry, not the best teacher out there )

 

[SpiralFlex]

Explanation coming up then.

 

[SpiralFlex]

When we have a univariate equation of a quadratic we are often to find these roots of the equation, either by factorisation and using null factor law or by the quadratic formula.

For example,







We call 2, 3 the roots (sometimes you hear the word zeros, used interchangeably) of the equation.



We will now define the roots to be alpha and beta. There are only two roots, why? Because this is derived from The Fundamental Theorem of Algebra which is

Every non-zero univariable polynomial with complex coefficients has exactly as many complex roots as its degree.

In simpler terms, a quadratic (degree two) has two complex roots. A cubic has three complex roots. But you don't learn the word "complex roots" until later in your studies. So for now we will agree that some quadratics will have two real roots.


Following the example above,

Let's try the sum of the roots,



We see we come up with a value of 5. Let's inspect the polynomial,




Doesn't this look like the second term but with a minus sign?



Let's try the product of the roots,




Let's inspect our polynomial again,



Doesn't this value of 6 agree with the constant term of the polynomial?



Let's see why.


We defined alpha, beta to be the roots of some quadratic equation say,







We can also write it in a products of sums form,






If these two expressions are equivalent, we can equate them. So -










By equating coefficients of x and the constants,



Sum of the roots:



Or sometimes written as,






Product of the roots,



Or sometimes written as




Alternatively,

Consider the quadratic equation,




We can find the roots by using the quadratic equation formula,





Of course alpha, beta are arbitrarily defined so they can be interchangeable.


Sum of roots,








Product of roots:



Using difference between squares in numerator,

 

[Demento1]

Proved the sum and product of roots using quadratic equation, based on spiral's answers, I think I am correct.

For my maths paper, I will post solutions once I can get somebody to combine all my PDF files into one to share onto a website link. Give me about a day and you can mark your papers according to my solutions and what I say deserve or doesn't deserve marks.

 

[Sy123]

Also I will add to Spiral's explanation.

Notice



The fact is, all this time when you were evaluating quadratic equations by using the rule: 'Find two numbers which when we add them you get the middle term and when we multiply them we get the constant'

Like when we factorise:



Lets find two numbers, which when you add them you get 5, when you times them you get 6. Its 2 and 3 right? So our factorised form is:



And hence our roots/zeroes/solutions will be -2 and -3.

Plug it into our formula

So -b/a should be -(-2-3)=5 which it is
and c/a should be 2*3=6 which it is

So I thought it would be useful to note that whenever you are actually doing this method of factorising quadratics, the heart of what you are doing is the sum and product of roots =)

 

[Demento1]

Here is the link for the exam that you can download (appreciations go to twinklegal for doing the sharing):

http://www.mediafire.com/view/?4mzelj1ik39clf6

And below are my solutions that I have for the exam (I've allocated what deserves and doesn't deserve the marks):

http://www.mediafire.com/view/?4j6ayx6mw5c9pr2

 

[chocolatelatte]

hehe yay thanks for sharing =)