Complex No.'s Question (1 Viewer)
- Thread starter Rono123
- Start date
Note the x/4 and 3x/4 should both be pie, this is from patel so i know which question it is
The first thing you do here is find all the 4 roots of -1 and notice that they occur in conjugate pairs, im sure you can get that far so ill go straight to the rootss:
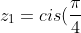 \\ z_{2}= cis(\frac{3\pi}{4}) \\ z_{3}=cis(\frac{5\pi}{4})=cis(\frac{-3\pi}{4}) \\ z_{4}=cis(\frac{7\pi}{4})=cis(\frac{-\pi}{4}))
we notice that z1 and z4 are conjugate pairs so are z2 and z3 therefore:
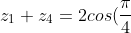 \\ z_{2} +z_{3}=2cos(\frac{3\pi}{4}) \\ z_{1}z_{4}=1 \\ z_{2}z_{3}=1)
Then we use the fact that we can express the original equation as the product of its factors:
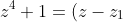(z-z_{4})(z-z_{2})(z-z_{3}))
i purposely put it into this form, so then we multipy the two brackets with the conjugate pairs and sub in the values we obtained above to get the first part of the question:
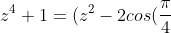z+1)(z^{2}-2cos(\frac{3\pi}{4})z + 1))
this is z^4 + 1 expressed in factors with real coefs...
to do the next part of the question we divide everything by z^2 as follows:
z+1)}{z}\frac{(z^{2}-2cos(\frac{3\pi}{4})z + 1)}{z})
we do this because the only way to get cos2x is to remember that:
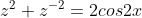
and we divide each invidual bracket by z so we can get z + z^-1 which will give cosx and we end up with:
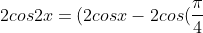)(2cosx-2cos(\frac{3\pi}{4})))
taking out the 2 from each bracket will give 4 on the RHS then dividing both sides by 2 gives the desired result:
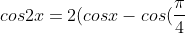)(cosx-cos(\frac{3\pi}{4})))
The first thing you do here is find all the 4 roots of -1 and notice that they occur in conjugate pairs, im sure you can get that far so ill go straight to the rootss:
we notice that z1 and z4 are conjugate pairs so are z2 and z3 therefore:
Then we use the fact that we can express the original equation as the product of its factors:
i purposely put it into this form, so then we multipy the two brackets with the conjugate pairs and sub in the values we obtained above to get the first part of the question:
this is z^4 + 1 expressed in factors with real coefs...
to do the next part of the question we divide everything by z^2 as follows:
we do this because the only way to get cos2x is to remember that:
and we divide each invidual bracket by z so we can get z + z^-1 which will give cosx and we end up with:
taking out the 2 from each bracket will give 4 on the RHS then dividing both sides by 2 gives the desired result: