Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Can you use induction for non induction qs? (1 Viewer)
- Thread starter 5uMath
- Start date
You can, since it is a method of proof, as long as it doesn't specify something else. Usually though, if it is to be solved by induction it will mention induction, so maybe have a look at other methods before then. If you do use induction though, from experience, markers will try as hard as they can to get rid of marks for you. The most common mistakes include:
1. Not choosing the correct base case (Actually a big issue, not as simple as it seems)
2. Not applying the inductive step correctly (Making a wrong assumption)
3. Wrong simplifications (Algebra)
4. Wrong logic (If you are using a logic argument, not accounting for a specific case)
It also depends on the math you are doing - what is the context for you? (I have no experience in 5u math sorry )
)
1. Not choosing the correct base case (Actually a big issue, not as simple as it seems)
2. Not applying the inductive step correctly (Making a wrong assumption)
3. Wrong simplifications (Algebra)
4. Wrong logic (If you are using a logic argument, not accounting for a specific case)
It also depends on the math you are doing - what is the context for you? (I have no experience in 5u math sorry
The question showed up in a BOS trial exam for 4 unit - I don't remember it that clearly but it was about proving 1 + 2x +3x^2 .... + nx^(n-1) = some expression in terms of x and n.You can, since it is a method of proof, as long as it doesn't specify something else. Usually though, if it is to be solved by induction it will mention induction, so maybe have a look at other methods before then. If you do use induction though, from experience, markers will try as hard as they can to get rid of marks for you. The most common mistakes include:
1. Not choosing the correct base case (Actually a big issue, not as simple as it seems)
2. Not applying the inductive step correctly (Making a wrong assumption)
3. Wrong simplifications (Algebra)
4. Wrong logic (If you are using a logic argument, not accounting for a specific case)
It also depends on the math you are doing - what is the context for you? (I have no experience in 5u math sorry)
My instinct was to use induction as it was a sequence, and proving that it converged to a certain function would have involved using maths outside the scope of the syllabus. Induction is a reasonable argument in this case.
For the problems you suggested:
1. From the series, you can deduce what the base case is (n=0 for this question, 1x^n = 1 => n=0)
2. Making the wrong assumption in this case would be very difficult as it just requires to say that S(n) =>S(k), for some k bounded by the same restrictions as n.
3. Thats not a problem in 5u math
4. For logical/non-algebraic arguments, I would suggest to stay away from induction unless otherwise stated in the question.
Induction is a valid method of proof and so perfectly acceptable, so long as the restriction to operating on the integers is valid. However, it is sometimes an inefficient approach that can cost you time rather than marks in an exam context.
For example:
1. I can use induction to prove that
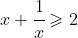
for all integers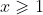
2.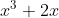 is a multiple of 3 for all positive integers
is a multiple of 3 for all positive integers  , which can be proven by induction.
, which can be proven by induction.
Both of these can be proven in 2-3 lines, without induction, and in the first case, prove the more general result for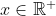 which is not provable by induction.
which is not provable by induction.
For example:
1. I can use induction to prove that
for all integers
2.
Both of these can be proven in 2-3 lines, without induction, and in the first case, prove the more general result for
Yes I would know how to prove both of them without the use of induction as it isnt necessary for any of them.Induction is a valid method of proof and so perfectly acceptable, so long as the restriction to operating on the integers is valid. However, it is sometimes an inefficient approach that can cost you time rather than marks in an exam context.
For example:
1. I can use induction to prove that
for all integers
2.is a multiple of 3 for all positive integers
, which can be proven by induction.
Both of these can be proven in 2-3 lines, without induction, and in the first case, prove the more general result forwhich is not provable by induction.
Suppose a statement were set up and you can identify two variables, one that would act as x and another as n, then prove for the valid set of n by induction.
Proving that a series converges to a specific function, for example, can be done much more efficiently than having to use induction by using summation formula for geomtric or arithmetic series, however induction would be a more valid approach as it assures for multiple cases, and because not all series are arithmetic or geometric. Even though induction is more time consuming, it is better off used in the cases where it certainly can be used.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
It is just the derivative of a finite GS. As there is a finite number of terms, why do you have the concern of convergence?The question showed up in a BOS trial exam for 4 unit - I don't remember it that clearly but it was about proving 1 + 2x +3x^2 .... + nx^(n-1) = some expression in terms of x and n.
My instinct was to use induction as it was a sequence, and proving that it converged to a certain function would have involved using maths outside the scope of the syllabus. Induction is a reasonable argument in this case.
For the problems you suggested:
1. From the series, you can deduce what the base case is (n=0 for this question, 1x^n = 1 => n=0)
2. Making the wrong assumption in this case would be very difficult as it just requires to say that S(n) =>S(k), for some k bounded by the same restrictions as n.
3. Thats not a problem in 5u math
4. For logical/non-algebraic arguments, I would suggest to stay away from induction unless otherwise stated in the question.
Last edited:
Its not GS the way its given to you. 3x/2 is not 4x/3, so there is no common difference unless you re arrange it. In the case where youre not bothered like me, induction should be fine.It is just the derivative of a finite GS. As there is a finite number of terms, why do you have the concern of convergence?
Sorry I used the term convergence a bit too broadly, what I meant is proving that it equals something, i.e. converges to a specific function.
Also im not specific to that question, my question was general but used this as an example.
Why does there have to be a common difference if you take the sum of a geometric sequence?Its not GS the way its given to you. 3x/2 is not 4x/3, so there is no common difference unless you re arrange it. In the case where youre not bothered like me, induction should be fine.
Sorry I used the term convergence a bit too broadly, what I meant is proving that it equals something, i.e. converges to a specific function.
Also im not specific to that question, my question was general but used this as an example.
Yeah, I just found my older solutions to the paper and thats what I did. Again i just used that as an example. Theres nothing wrong with induction though in the case where you dont immediately recognise something.It is just the derivative of a finite GS. As there is a finite number of terms, why do you have the concern of convergence?
The limitting sum is a/(1-r) and the sum to n terms is a(1-r^n)/(1-r), where r is the common difference. The common difference for a gp is achieved by dividing nth term by n-1 term, and if this quotient is consistent for more than one pair of terms, then the series is gp. The way in which the common difference is given is what differentiates between arithmetic and geometric.Why does there have to be a common difference if you take the sum of a geometric sequence?
What was said is that you use this formula to solve for 1 + x + x^2 + x^3... x^n - say this is AYeah, I just found my older solutions to the paper and thats what I did. Again i just used that as an example. Theres nothing wrong with induction though in the case where you dont immediately recognise something.
Then after summing this, you derive both sides. On the LHS, you get:
1 + 2x + 3x^2 + 4x^3 + .... (What the question asks)
On the RHS, you get the derivative of A. That is your answer.
EDIT - Yeah, I realise this was said.
You mean differentiate both sides? Cause derive is completely different.What was said is that you use this formula to solve for 1 + x + x^2 + x^3... x^n - say this is A
Then after summing this, you derive both sides. On the LHS, you get:
1 + 2x + 3x^2 + 4x^3 + .... (What the question asks)
On the RHS, you get the derivative of A. That is your answer.
EDIT - Yeah, I realise this was said.
If thats what you mean, then yes, I also said that I did use differentiation initially to obtain the result... my comment was simply that mathematical induction is still valid.
When I looked at the question a second time months later, I did not remember that I used differentiation and my instinct was to use induction, which is still completely valid.
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
I agree induction is fine.Its not GS the way its given to you. 3x/2 is not 4x/3, so there is no common difference unless you re arrange it. In the case where youre not bothered like me, induction should be fine.
Sorry I used the term convergence a bit too broadly, what I meant is proving that it equals something, i.e. converges to a specific function.
Also im not specific to that question, my question was general but used this as an example.
By the way, we have common "difference" in AS and common "ratio" in GS.
Oops ahaha thanks. Forgot about that, but they are both a difference of some sort. SorryI agree induction is fine.
By the way, we have common "difference" in AS and common "ratio" in GS.
