The square has length
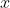
. Its perimeter, which is the amount of wire used to make the square, must therefore be
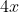
.
The remaining amount of wire,
 cm
cm (not
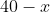
), is used to make the circumference of the circle (
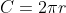
).
You now know the radius of the circle and the side length of the square, so you can find the area of both shapes now.

When you find
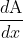
, notice that the required expression is
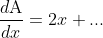
, so the hint is that you should leave the expression as is without expanding the term in the square or combining fractions.
^2 )
You can take out the constant in the second term's denominator
^2)
and differentiate using the chain rule, which will give you the required answer.


