Calculus & Analysis Marathon & Questions (1 Viewer)
- Thread starter porcupinetree
- Start date
Paradoxica
-insert title here-
Re: First Year Uni Calculus Marathon
f(x,y) = a(x+y) + b
a,b ∈ ℝ
For an infinitely differentiable class, the trigonometric functions, their inverses, the hyperbolic functions, their inverses, the exponential function and it's inverse, all result in valid examples.
...Actually pretty much any function with above as argument is a valid example...
Proof by direct example, for once differentiable:
f(x,y) = a(x+y) + b
a,b ∈ ℝ
For an infinitely differentiable class, the trigonometric functions, their inverses, the hyperbolic functions, their inverses, the exponential function and it's inverse, all result in valid examples.
...Actually pretty much any function with above as argument is a valid example...
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Re: First Year Uni Calculus Marathon
Am I misinterpreting the sequence? Cause I'm getting a2k=n, a2k+1=1_{n>0}$ be defined by the following: $ \\\\ a_1 = 1, a_{n+1} = \frac{n}{a_n} )
Paradoxica
-insert title here-
Re: First Year Uni Calculus Marathon
roll a d10
...maybe you should perform a sanity check...
roll a d10
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: First Year Uni Calculus Marathon
A glimpse of one of the first subtleties of measure theory:
Consider the set of points on the unit circle C.
Suppose we want a way of measuring the size/length of arbitrary subsets of C. I.e. we want a function m that maps arbitrary subsets of C to non-negative real numbers.
What properties should such a function have?
P1. We certainly would hope that m is rotationally invariant. I.e. we need m(R(A))=m(A) for arbitrary rotations R of the circle.
P2. We would also like the size of the sum of disjoint subsets to be equal to the sum of the sizes of the individual subsets. That is, we require
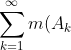=m\left(\cup_{k=1}^\infty A_k\right))
if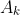
are pairwise disjoint subsets of 
.
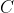One of the axioms of mathematics is the axiom of choice:
(AC) Given an arbitrary collection of nonempty sets sets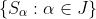
where J is an index set, there exists a function 
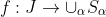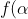such that \in S_\alpha)
. Informally, this says that given an indexed collection of nonempty sets, we can choose an element from each set and lump these together to form a new set. (This does NOT follow from the other axioms of set theory.)
Problem: Prove that there does not exist such a function m satisfying the properties P1 and P2.
Hint: (AC) is key. Use a clever equivalence relation and (AC) to assemble a sets that lead to contradictions with P1 and P2. If you post partial progress, I can provide further hints.
A glimpse of one of the first subtleties of measure theory:
Consider the set of points on the unit circle C.
Suppose we want a way of measuring the size/length of arbitrary subsets of C. I.e. we want a function m that maps arbitrary subsets of C to non-negative real numbers.
What properties should such a function have?
P1. We certainly would hope that m is rotationally invariant. I.e. we need m(R(A))=m(A) for arbitrary rotations R of the circle.
P2. We would also like the size of the sum of disjoint subsets to be equal to the sum of the sizes of the individual subsets. That is, we require
if
One of the axioms of mathematics is the axiom of choice:
(AC) Given an arbitrary collection of nonempty sets sets
Problem: Prove that there does not exist such a function m satisfying the properties P1 and P2.
Hint: (AC) is key. Use a clever equivalence relation and (AC) to assemble a sets that lead to contradictions with P1 and P2. If you post partial progress, I can provide further hints.
Paradoxica
-insert title here-
help i'm trapped in a forum factory
}$ is a sequence such that $\sum_{n>0} x_n < \infty \\ $Prove $ \sum_{n>0} (e^{x_n}-1) < \infty)
Paradoxica
-insert title here-
Re: First Year Uni Calculus Marathon
x_{n}-y_{n}+4}{n}, y_{n+1}=\frac{(n-1)y_{n}-x_{n}+3}{n})
How do I prove the sequences converge? I already know what it converges to, so that's not the issue here.
How do I prove the sequences converge? I already know what it converges to, so that's not the issue here.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,662
- Gender
- Male
- HSC
- 2007
Re: First Year Uni Calculus Marathon
Here is one instructive way to do it (probably not the fastest way):
First choose more natural coordinates, u_n=x_n-1, v_n=y_n-2 centred at the fixed point.
Our recurrence then transforms to:
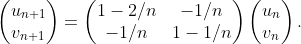
The matrix in question is symmetric, which implies that the eigenvalues are real and the eigenspaces are orthogonal. (An easy computation shows that there are indeed two distinct eigenvalues.)
A consequence of this fact is that these matrix satisfies
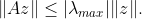
(Exercise).
The maximal (maximal means maximal in absolute value btw) eigenvalue of the n-th matrix is
)
and so convergence of (u_n,v_n) to 0 is proven by showing that the product of these maximal eigenvalues tends to zero, which I am sure you are capable of.
(*) Note that this method establishes convergence for ANY choice of initial point (x_0,y_0). Note also that this is quite related to my most recently posted problem in the linear algebra marathon, which addresses sequences like this but for a fixed multiplication matrix (which is not specified and need not be symmetric).
Here is one instructive way to do it (probably not the fastest way):
First choose more natural coordinates, u_n=x_n-1, v_n=y_n-2 centred at the fixed point.
Our recurrence then transforms to:
The matrix in question is symmetric, which implies that the eigenvalues are real and the eigenspaces are orthogonal. (An easy computation shows that there are indeed two distinct eigenvalues.)
A consequence of this fact is that these matrix satisfies
(Exercise).
The maximal (maximal means maximal in absolute value btw) eigenvalue of the n-th matrix is
and so convergence of (u_n,v_n) to 0 is proven by showing that the product of these maximal eigenvalues tends to zero, which I am sure you are capable of.
(*) Note that this method establishes convergence for ANY choice of initial point (x_0,y_0). Note also that this is quite related to my most recently posted problem in the linear algebra marathon, which addresses sequences like this but for a fixed multiplication matrix (which is not specified and need not be symmetric).
Last edited:
Paradoxica
-insert title here-
Re: First Year Uni Calculus Marathon
 \varphi(k) = \frac{6}{\pi^2} \int_0^1 x f(x) \text{d}x)
Bonus: Come up with a general statement that extends to any arithmetical function that has a sufficiently "nice" asymptotic approximation.
Bonus: Come up with a general statement that extends to any arithmetical function that has a sufficiently "nice" asymptotic approximation.
Last edited:
Re: First Year Uni Calculus Marathon
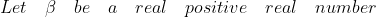
{ a }_{ k } } =L\int _{ 0 }^{ 1 }{ \beta { x }^{ \beta -1 }f(x)\quad dx } \\ Now\quad we\quad know\quad \\ \lim _{ n\xrightarrow { } \infty }{ \frac { 1 }{ { n }^{ 2 } } } \sum _{ k=1 }^{ n }{ \varphi (k) } =\frac { 3 }{ { \pi }^{ 2 } } \\ \therefore \lim _{ n\xrightarrow { } \infty }{ \frac { 1 }{ { n }^{ 2 } } } \sum _{ k=1 }^{ n }{ f(\frac { k }{ n } )\varphi (k) } =\frac { 6 }{ { \pi }^{ 2 } } \int _{ 0 }^{ 1 }{ { x }f(x)\quad dx } \quad as\quad L=\frac { 3 }{ { \pi }^{ 2 } } and\quad \beta =2)
Bonus: Come up with a general statement that extends to any arithmetical function that has a sufficiently "nice" asymptotic approximation.
Last edited: